
科目: 来源: 题型:
【题目】)甲乙两人在相同条件下完成了5次射击训练,两人的成绩如图所示.
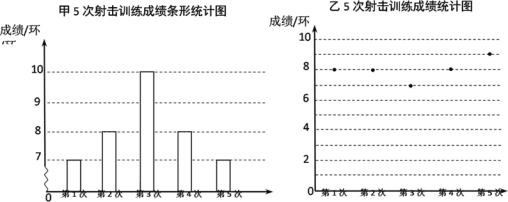
(1)甲射击成绩的众数为 环,乙射击成绩的中位数为 环;
(2)计算两人射击成绩的方差;
(3)根据训练成绩,你认为选派哪一名队员参赛更好,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,线段AB的长度为2,AB所在直线上方存在点C,使得△ABC为等腰三角形,设△ABC的面积为S.当S=___________时,满足条件的点C恰有三个.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠B=36°,点D为斜边BC的中点,将线段DC绕着点D逆时针旋转任意角度得到线段DE(点E不与A、B、C重合),连接EA,EC,则∠AEC=___________°.
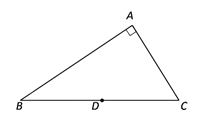
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 抛物线的顶点.
抛物线的顶点.
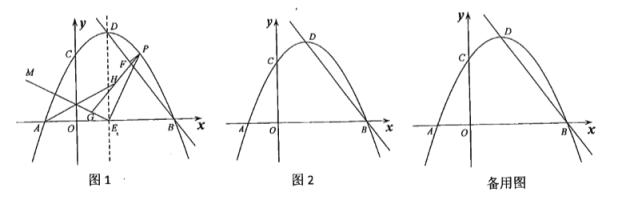
(1)求直线![]() 的解析式;
的解析式;
(2)抛物线对称轴交![]() 轴于点
轴于点![]() ,
,![]() 为直线
为直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,当线段
,当线段![]() 的长最大时,连接
的长最大时,连接![]() ,过点
,过点![]() 作射线
作射线![]() ,且
,且![]() ,点
,点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)如图2,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() ,
,![]() 平移后的对应点分别为点
平移后的对应点分别为点![]() ,
,![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 是否能为等腰直角三角形?若能,请求出所有符合条件的
是否能为等腰直角三角形?若能,请求出所有符合条件的![]() 点的坐标;若不能,请说明理由.
点的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】初中数学代数知识中,方程、函数、不等式存在着紧密的联系,请阅读下列两则材料,回答问题:
利用函数图象找方程![]() 解的范围.设函数
解的范围.设函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .则函数
.则函数![]() 的图象经过两个点
的图象经过两个点![]() 与
与![]() ,而点
,而点![]() 在
在![]() 轴下方,点
轴下方,点![]() 在
在![]() 轴上方,则该函数图象与
轴上方,则该函数图象与![]() 轴交点横坐标必大于-2,小于-1.故,方程
轴交点横坐标必大于-2,小于-1.故,方程![]() 的有解,且该解的范围为
的有解,且该解的范围为![]() .
.
材料二:
解一元二次不等式![]() .由“异号两数相乘,结果为负可得:
.由“异号两数相乘,结果为负可得:
情况①![]() ,得
,得![]() ,则
,则![]()
情况②![]() ,得
,得![]() ,则无解
,则无解
故,![]() 的解集为
的解集为![]() .
.
(1)请根据材料一解决问题:已知方程![]() 有唯一解
有唯一解![]() ,且
,且![]() (
(![]() 为整数),求整数
为整数),求整数![]() 的值.
的值.
(2)请结合材料一与材料二解决问题:若关于![]() 的方程
的方程![]() 的解分别为
的解分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】闺蜜装在大学校园里盛行,闺蜜装能很好的表达“亲如姐妹”的友谊,也能成为校园一道靓丽的风景.某专卖店购进一批![]() ,
,![]() 两款闺蜜装,共花费了18400元,
两款闺蜜装,共花费了18400元,![]() 款比
款比![]() 款多20套,其中每套
款多20套,其中每套![]() 款闺蜜装进价200元,每套
款闺蜜装进价200元,每套![]() 款闺蜜装进价160元.进行试销售,供不应求,很快销售完毕,己知每套
款闺蜜装进价160元.进行试销售,供不应求,很快销售完毕,己知每套![]() 款闺蜜装售价为240元.
款闺蜜装售价为240元.
(1)求购进![]() ,
,![]() 两款闺蜜装各多少套?
两款闺蜜装各多少套?
(2)国庆将至,专卖店又购进第二批![]() ,
,![]() 两款闺蜜装并进行促销活动,在促销期间,每套
两款闺蜜装并进行促销活动,在促销期间,每套![]() 款闺蜜装在进价的基础上提高
款闺蜜装在进价的基础上提高![]() 销售,每套
销售,每套![]() 款闺蜜装在第一批售价的基础上降低
款闺蜜装在第一批售价的基础上降低![]() 销售,结果在促销售活动中,
销售,结果在促销售活动中,![]() 款闺蜜装的销量比第一批
款闺蜜装的销量比第一批![]() 款销售量降低了
款销售量降低了![]() ,
,![]() 款闺蜜装的销售量比第一批
款闺蜜装的销售量比第一批![]() 款销售量上升了
款销售量上升了![]() ,结果本次促销活动共获利5200元,求
,结果本次促销活动共获利5200元,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为常数且
为常数且![]() ).已知当
).已知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.

请参照学习函数的过程和方法对该函数进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量![]() 取值范围;
取值范围;
(2)请在下列平面直角坐标系中补全该函数的图象;
(3)请你在上方直角坐标系中画出函数![]() 的图像,结合上述函数的图象,写出不等式
的图像,结合上述函数的图象,写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是第一象限内抛物线上的一个动点(与点
是第一象限内抛物线上的一个动点(与点![]() ,
,![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,直线
,直线![]() 能否把
能否把![]() 分成面积之比为2:3的两部分?若能,请求出点
分成面积之比为2:3的两部分?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com