
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
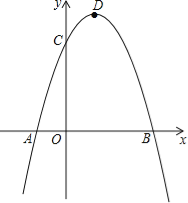
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3)三点.

(1)求这个二次函数的解析式.
(2)在抛物线上存在一点P使△ABP的面积为10,求点P的坐标.(写出详细的解题过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
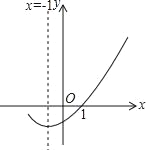
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
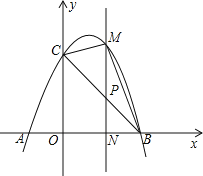
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)若点![]() 为线段
为线段![]() 上的一点(不与
上的一点(不与![]() 、
、![]() 重合),
重合),![]() 轴,且
轴,且![]() 交抛物线于点
交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 的面积最大时,求
的面积最大时,求![]() 的周长.
的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动.

(1)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的面积等于
的面积等于![]() ?
?
(2)如果![]() 分别从
分别从![]() 同时出发,
同时出发,![]() 的面积能否等于
的面积能否等于![]() ?
?
(3)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的长度等于
的长度等于![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
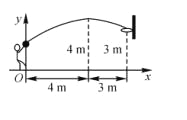
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市正大力发展绿色农产品,有一种有机水果A特别受欢迎,某超市以市场价格10元/千克在该市收购了6000千克A水果,立即将其冷藏,请根据下列信息解决问题:
①水果A的市场价格每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天.
(1)若将这批A水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为_____元;可以出售的完好水果还有_____千克;
天后这批水果的销售单价为_____元;可以出售的完好水果还有_____千克;
(2)将这批A水果存放多少天后一次性出售所得利润为9600元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=![]() x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=![]() 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
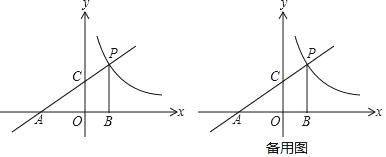
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=![]() 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
(3)设点R在反比例函数y=![]() 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com