
科目: 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,BC=m,D,E分别是AB,AC边的中点,点P为BC边上的一个动点,连接PD,PA,PE.设PC=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线可能是( )

A.PBB.PEC.PAD.PD
查看答案和解析>>
科目: 来源: 题型:
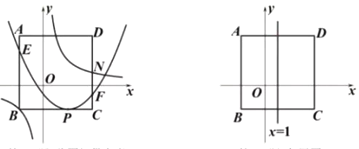
【题目】在平面直角坐标系中,正方形ABCD的四个顶点坐标分别为A(-2,4),B(-2,-2),C(4,-2),D(4,4).
(1)填空:正方形的面积为_______;当双曲线![]() (k≠0)与正方形ABCD有四个交点时,k的取值范围是_______.
(k≠0)与正方形ABCD有四个交点时,k的取值范围是_______.
(2)已知抛物线L:![]() (a>0)顶点P在边BC上,与边AB,DC分别相交于点E,F,过点B的双曲线
(a>0)顶点P在边BC上,与边AB,DC分别相交于点E,F,过点B的双曲线![]() (k≠0)与边DC交于点N.
(k≠0)与边DC交于点N.
①点Q(m,-m2-2m+3)是平面内一动点,在抛物线L的运动过程中,点Q随m运动,分别求运动过程中点Q在最高位置和最低位置时的坐标.
②当点F在点N下方,AE=NF,点P不与B,C两点重合时,求![]() 的值.
的值.
③求证:抛物线L与直线![]() 的交点M始终位于
的交点M始终位于![]() 轴下方.
轴下方.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:三角形ABC内接于圆O,∠BAC与∠ABC的角平分线AE,BE相交于点E,延长AE交外接圆O于点D,连接BD,DC,且∠BCA=60°

(1)求∠BED的大小;
(2)证明:△BED为等边三角形;
(3)若∠ADC=30°,圆O的半径为r,求等边三角形BED的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,点A是抛物线与x轴的另一个交点.
经过B,C两点,点A是抛物线与x轴的另一个交点.
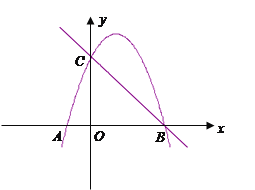
(1)求出点B和点C的坐标.
(2)求此抛物线的函数解析式.
(3)在抛物线x轴上方存在一点P(不与点C重合),使![]() ,请求出点P的坐标.
,请求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
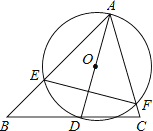
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
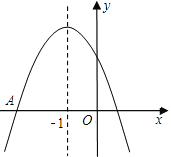
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.


(1)求抛物线的解析式及顶点D的坐标;
(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;
(3)若点Q为线段OC上的一动点,问:AQ+![]() QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() 箱与销售价
箱与销售价![]() 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com