
科目: 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 分别从
分别从![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,两点停止运动,设运动时间为
时,两点停止运动,设运动时间为![]() 秒.
秒.
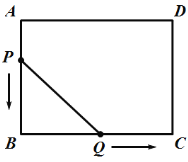
(1)填空:![]() __________,
__________,![]() _________;(用含
_________;(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() 的长度等于
的长度等于![]() ?
?
(3)当![]() 为何值时,五边形
为何值时,五边形![]() 的面积有最小值?最小值为多少?
的面积有最小值?最小值为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】赣州蓉江新区某汽车销售公司去年12月份销售新上市一种新型低能耗汽车200辆,由于该型汽车的优越的经济适用性,销量快速上升,今年2月月份该公司销售该型汽车达到450辆,并且去年12月到今年1月和今年1月到2月两次的增长率相同.
(1)求该公司销售该型汽车每次的增长率;
(2)若该型汽车每辆的盈利为5万元,则平均每天可售8辆,为了尽量减少库存,汽车销售公司决定采取适当的降价措施,经调查发现,每辆汽车每降5000元,公司平均每天可多售出2辆,若汽车销售公司每天要获利48万元,每辆车需降价多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别在线段BC和CD上,![]() .连接EF。将△ADF绕着点顺时针旋转90°,得到
.连接EF。将△ADF绕着点顺时针旋转90°,得到![]()
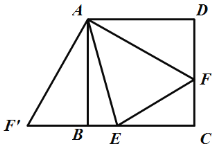
(1)证明:![]()
(2)证明:EF=BE+DF.
(3)已知正方形ABCD边长是6,EF=5,求线段BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】作图题:在图(1)(2)所示抛物线中,抛物线与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() ,点
,点![]() 是抛物线的顶点,过
是抛物线的顶点,过![]() 平行于
平行于![]() 轴的直线是它的对称轴,点
轴的直线是它的对称轴,点![]() 在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:
在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:
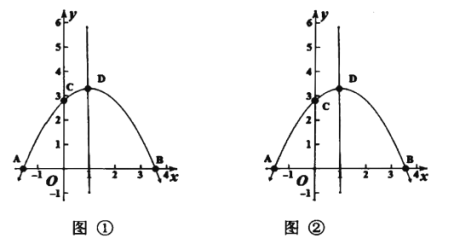
(1)在图①中作出点![]() ,使线段
,使线段![]() 最小;
最小;
(2)在图②中作出点![]() ,使线段
,使线段![]() 最大.
最大.
查看答案和解析>>
科目: 来源: 题型:
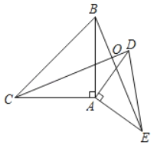
【题目】如图,△ABC与△ADE都是等腰直角三角形,连接CD、BE,CD、BE相交于点O,△BAE可看作是由△CAD顺时针旋转所得.
(1)旋转中心是 ,旋转角度是 ;
(2)判断CD与BE的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
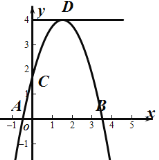
【题目】如图,抛物线顶点为A(1,2),且过原点,与x轴的另一个交点为B,

(1)求抛物线的解析式和B点坐标;
(2)抛物线上是否存在点M,使△OBM的面积等于2?若存在,请写出M点坐标,若不存在,说明理由;
查看答案和解析>>
科目: 来源: 题型:
【题目】两块不同的三角板按如图所示摆放,两个直角顶点C重合,![]() ,
,![]() 。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.
。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() ,且
,且![]() 、
、![]() 位于原点两侧,与
位于原点两侧,与![]() 的正半轴交于
的正半轴交于![]() ,顶点
,顶点![]() 在
在![]() 轴右侧的直线
轴右侧的直线![]() :
:![]() 上,则下列说法:①
上,则下列说法:①![]() ②
②![]() ③
③![]() ④
④![]() 其中正确的结论有( )
其中正确的结论有( )
A.①②B.②③C.②③④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式;
(2)若点![]() 在第一象限的抛物线上,且点
在第一象限的抛物线上,且点![]() 的横坐标为
的横坐标为![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值;
的最大值;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形为等腰三角形?如果存在,直接写出
为顶点的三角形为等腰三角形?如果存在,直接写出![]() 点坐标;如果不存在,请说明理由.
点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com