练习册

  • 练习册
  • 试题
    相关习题
     0  364204  364212  364218  364222  364228  364230  364234  364240  364242  364248  364254  364258  364260  364264  364270  364272  364278  364282  364284  364288  364290  364294  364296  364298  364299  364300  364302  364303  364304  364306  364308  364312  364314  364318  364320  364324  364330  364332  364338  364342  364344  364348  364354  364360  364362  364368  364372  364374  364380  364384  364390  364398  366461 

    科目： 来源： 题型：

    【题目】已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB＝AC，连接AC，过点D作DE⊥AC，垂足为 E．

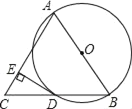
    （1）求证：DC＝BD；

    （2）求证：DE为⊙O的切线；

    （3）若AB＝12，AD＝6，连接OD，求扇形BOD的面积．

    查看答案和解析>>

    科目： 来源： 题型：

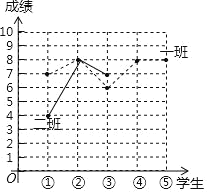
    【题目】垫球是排球队常规训练的重要项目之一，也是我市初中体育学业水平考试的一个选考项目．下列图表中的数据是从九年级一班、二班各随机抽取五名学生垫球测试成绩：

    测试学生序号

    ①

    ②

    ③

    ④

    ⑤

    一班

    7

    8

    6

    7

    7

    二班

    4

    8

    7

    10

    6

    解答下列问题：

    （1）一班五名学生的测试成绩的众数是　 　，二班五名学生的测试成绩的中位数是　 　．

    （2）请你在图中补全二班五名学生的垫球测试成绩的折线统计图．从题中的信息，估计　 　班的垫球成绩要稳定．

    （3）把前三次对应序号下一班学生的垫球测试成绩减去二班学生垫球测试成绩，分别可得到数字3、0、﹣1，从这三个数中任意选取两个数组成有序数对（x，y），请用列表法或画树状图法列出可能出现的结果，并计算点（x，y）落在二次函数y＝x2﹣1的图象上的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在△ABC中，AC＝BC，∠ACB＝90°，直线l经过直角顶点C，AD⊥l，BE⊥l，垂足分别为D、E．

    （1）如图，若AD＝1，BE＝3，求DE的长度．

    （2）当直线l绕C点转动时，若AD＝a，BE＝b．请画出示意的图形并用含a、b的代数式直接表示出DE的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】四边形ABCD内接于⊙O，连接AC、BD，2∠BDC+∠ADB＝180°．

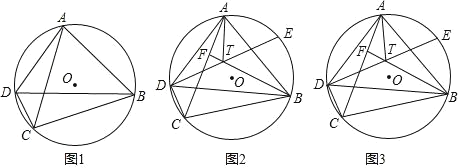
    （1）如图1，求证：AC＝BC；

    （2）如图2，E为⊙O上一点， ＝，F为AC上一点，DE与BF相交于点T，连接AT，若∠BFC＝∠BDC+∠ABD，求证：AT平分∠DAB；

    （3）在（2）的条件下，DT＝TE，AD＝8，BD＝12，求DE的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，∠BAC＝120°，点D为AB边上一点（不与点B重合），连接CD，将线段CD绕点D逆时针旋转90°，点C的对应点为E，连接BE．若AB＝2，则△BDE面积的最大值为_____．

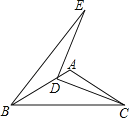
    查看答案和解析>>

    科目： 来源： 题型：

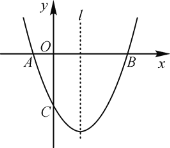
    【题目】如图，已知抛物线y＝ax2＋bx＋c（a≠0）经过A（－1，0），B（3，0），C（0，－3）三点，直线l是抛物线的对称轴．

    (1)求抛物线的函数解析式；

    (2)设点M是直线l上的一个动点，当点M到点A，点C的距离之和最短时，求点M的坐标；

    (3)在抛物线上是否存在点N，使S⊿ABN=S⊿ABC，若存在，求出点N的坐标，若不存在，说明理由.

    查看答案和解析>>

    科目： 来源： 题型：

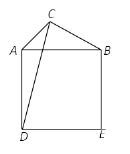
    【题目】如图,已知线段 AC=4,线段BC绕点C旋转,且BC=6,连结AB,以AB为边作正方形ADEB,连结CD.

    （1）若∠ACB=90°,则AB的值是____；

    （2）线段CD长的最大值是____．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在半径为6的⊙O中，正六边形ABCDEF与正方形AGDH都内接于⊙O，则图中阴影部分的面积为（　　）

    A. 27﹣9B. 18C. 54﹣18D. 54

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】二次函数的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④其顶点坐标为（，﹣2）；⑤当x＜时，y随x的增大而减小；⑥a+b+c＞0正确的有（　　）

    A. 3个 B. 4个 C. 5个 D. 6个

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】四边形ABCD内接于⊙O，连接AC、BD，2∠BDC+∠ADB＝180°．

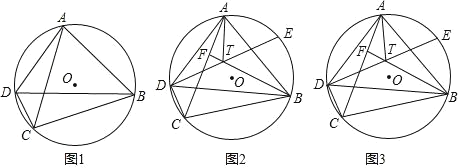
    （1）如图1，求证：AC＝BC；

    （2）如图2，E为⊙O上一点， ＝，F为AC上一点，DE与BF相交于点T，连接AT，若∠BFC＝∠BDC+∠ABD，求证：AT平分∠DAB；

    （3）在（2）的条件下，DT＝TE，AD＝8，BD＝12，求DE的长．

    查看答案和解析>>

    同步练习册答案