
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3(a≠0,且a,b为常数)的图象经过点(2,1)和(3,0).
(1)试求这条抛物线的解析式;
(2)若将抛物线进行上、下或左、右平移,请你写出一种平移的方法,使平移后的抛物线顶点落在直线y=x上,并直接写出平移后抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
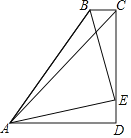
【题目】如图,四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°,若CD=4,则DE长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变最x和对应函数值y1,y2的部分对应值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时,自变量x的取值范图是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.

(1)画出△A1OB1;
(2)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ABCD,DEFG都是正方形,边长分别为m,n(m<n).坐标原点O为AD的中点,A,D,E在y轴上,若二次函数y=ax2的图象过C,F两点,则![]() =( )
=( )

A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() ﹣1D.2
﹣1D.2![]() ﹣1
﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知⊙O是以数轴的原点O为圆心,以3为半径的圆,∠AOB=45°,点P在数轴上运动.若过点P与OA平行的直线与⊙O有公共点,设点P在数轴上表示的数为x.则x的取值范围是( )

A.0≤x≤3![]() B.x>3
B.x>3![]() C.﹣3≤x≤3D.﹣3
C.﹣3≤x≤3D.﹣3![]() ≤x≤3
≤x≤3![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=![]() ,y=﹣2018x2+2019,y=2018x2共有的性质是( )
,y=﹣2018x2+2019,y=2018x2共有的性质是( )
A.开口向上
B.对称轴是y轴
C.当x>0时,y随x的增大而增大
D.都有最低点
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在等腰![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动,动点
匀速运动,动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动,设运动时间为
同时停止运动,设运动时间为![]()
![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为边作平行四边形
为边作平行四边形![]() .
.
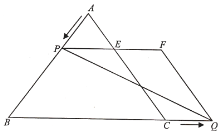
(1)当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的平分线上?若存在,求出
的平分线上?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有多少种不同的选择方法?
,有多少种不同的选择方法?
(问题探究)为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,再逐次递进,最后得出一般性的结论.
探究一:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,会有多少种不同的选择方法?
个连续的自然数,会有多少种不同的选择方法?
当![]() ,
,![]() 时,显然有
时,显然有![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有
时,有![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 这
这![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有________种不同的选择方法;
时,有________种不同的选择方法;

……
由上可知:从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法.
个连续的自然数,有_______种不同的选择方法.
探究二:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个,
个,![]() 个……
个……![]()
![]() 个连续的自然数,分别有多少种不同的选择方法?
个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空.
|
|
| ... |
|
|
|
|
|
|
|
|
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
由上可知:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]()
![]() 个连续的自然数,有______种不同的选择方法.
个连续的自然数,有______种不同的选择方法.
(问题解决)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有_______种不同的选择方法.
,有_______种不同的选择方法.
(实际应用)我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上,他共有______种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排![]() 号到
号到![]() 号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
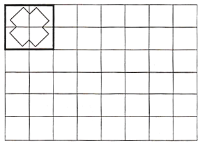
(拓展延伸)如图,将一个![]() 的图案放置在
的图案放置在![]() 的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com