
科目: 来源: 题型:
【题目】将正面分别标有数字![]() ,
,![]() ,
,![]() ,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求这张卡片上的数字为偶数的概率;
(2)随机地抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数恰好为“![]() ”的概率是多少?
”的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值:
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
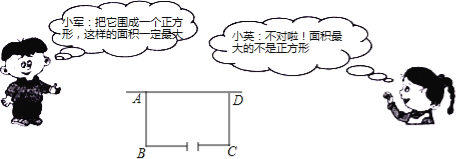
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①b2>4ac ②2a+b=0 ③c﹣a<0 ④若点B(﹣4,y1)、C(1,y2)为函数图象上的两点,则y1<y2,其中正确结论是( )
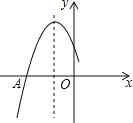
A.②④ B.②③ C.①③ D.①④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是_____________.
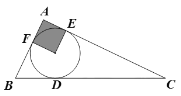
查看答案和解析>>
科目: 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,
(1)当顶点坐标为(2,2)时,求此函数的解析式;
(2)继续探究,如果b≠0,且抛物线顶点坐标为(m,m),m≠0,求此函数的解析式(用含m的式子表示)
(3)现有一组过原点的抛物线,顶点A1,A2,An在直线y=x上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,…,Bn,以线段AnBn为边向右作正方形AnBnnDn,若这组抛物线中有一条经过Dn,求所有满足条件的正方形边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
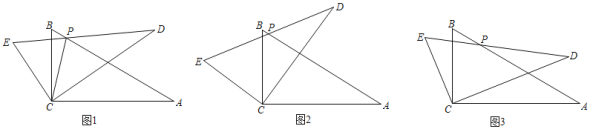
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com