【题目】材料：思考的同学小斌在解决连比等式问题：“已知正数，，满足，求的值”时，采用了引入参数法，将连比等式转化为了三个等式，再利用等式的基本性质求出参数的值.进而得出，，之间的关系，从而解决问题.过程如下：

解；设，则有：

，，，

将以上三个等式相加，得.

，，都为正数，

，即，.

.

仔细阅读上述材料，解决下面的问题：

（1）若正数，，满足，求的值；

（2）已知，，，互不相等，求证：.

【题目】已知函数y＝+b（a、b为常数且a≠0）中，当x＝2时，y＝4；当x＝﹣1时，y＝1．请对该函数及其图象进行如下探究：

（1）求该函数的解析式，并直接写出该函数自变量x的取值范围；

（2）请在下列直角坐标系中画出该函数的图象；

（3）请你在上方直角坐标系中画出函数y＝2x的图象，结合上述函数的图象，写出不等式+b≤2x的解集．

A.27米B.31米C.48米D.52米

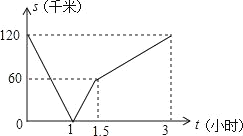
A.出发1小时时，甲、乙在途中相遇

B.出发1.5小时时，乙比甲多行驶了60千米

C.出发3小时时，甲、乙同时到达终点

D.甲的速度是乙速度的一半

【题目】如图，在矩形中，厘米，厘米. 点沿边从开始向点以2厘米/秒的速度移动；点沿边从点开始向点以1厘米/秒速度移动.如果、同时出发，用（秒）表示移动的时间，那么：

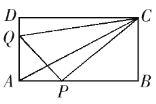
（1）当为何值时，为等腰直角三角形？

（2）求四边形的面积；提出一个与计算结果有关的结论；

（3）当为何值时，以点、、为顶点的三角形与相似？

【题目】如图，直线与轴交于点，与双曲线交于点，其中点在第一象限，点在第三象限。

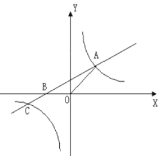
（1）求双曲线的解析式；

（2）求点的坐标；

（3）若，在轴上是否存在点，使是等腰三角形？若存在，请写出点的坐标；若不存在，请说明理由。

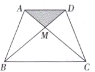
【题目】某村计划在新农村改造过程中，拟筹资金2000元，计划在一块上、下底分别为10米、20米的梯形空地上种植花草（如图所示，)，村委会想在地带与地带种植单价为10元的太阳花，当地带种满花后，已经花了500元，请你计算一下，若继续在地带种植同样的太阳花，资金是否够用？并说明理由.