
科目: 来源: 题型:
【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线“等边抛物线”.
(1)若对任意m,n,点M(m,n)和点N(-m+4,n)恒在“等边抛物线”![]() :
:![]() 上,求抛物线
上,求抛物线![]() 的解析式;
的解析式;
(2)若抛物线![]() :
:![]() “等边抛物线”,求
“等边抛物线”,求![]() 的值;
的值;
(3)对于“等边抛物线”![]() :
:![]() ,当1<x<m吋,总存在实数b。使二次函数
,当1<x<m吋,总存在实数b。使二次函数![]() 的图象在一次函数y=x图象的下方,求m的最大值.
的图象在一次函数y=x图象的下方,求m的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
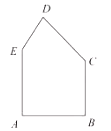
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
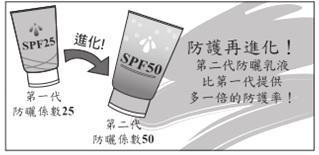
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.解答要求如下:
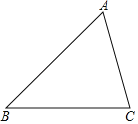
(1)对于图中△ABC,用尺规作出一条中位线DE;(不必写作法,但应保留作图痕迹)
(2)根据(1)中作出的中位线,写出已知,求证和证明过程.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确
B. 乙的结果正确
C. 甲、乙的结果合在一起才正确
D. 甲、乙的结果合在一起也不正确
查看答案和解析>>
科目: 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题:
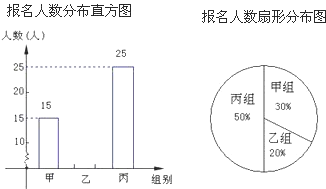
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目: 来源: 题型:
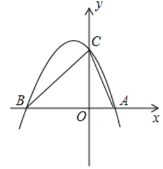
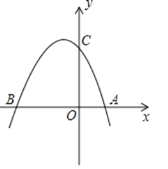
【题目】如图,抛物线y=﹣x2+mx+2与x轴交于点A,B,与y轴交于点C,点A的坐标为(1,0)
(1)求抛物线的解析式
(2)在抛物线的对称轴l上找一点P,使PA+PC的值最小,求出点P的坐标
(3)在第二象限内的抛物线上,是否存在点M,使△MBC的面积是△ABC面积的![]() ?若存在,求出点M的坐标,若不存在,请说明理由.
?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
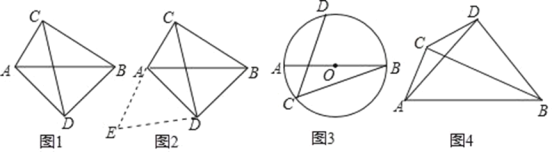
【题目】(问题背景)如图1,在四边形ADBC中,∠ACB=∠ADB=90o,AD=BD, 探究线段AC,BC,CD之间的数量关系
小明同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90o到△AED处,点B,C分别 落在点A,E处(如图2),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD
CD
(简单应用)
(1)在图1中,若AC=6,CD=![]() ,则AB= .
,则AB= .
(2)如图3,AB是⊙O的直径,点C.D在⊙O上,∠C=45o,若AB=25,BC=24,求CD的长.
(拓展延伸)
(3)如图4,∠ACB=∠ADB=90o,AD=BD,若AC=![]() ,CD=
,CD=![]() ,求BC的长.(用含
,求BC的长.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com