
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)设该抛物线的顶点为![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)设抛物线上的点![]() 在第一象限,
在第一象限,![]() 是以
是以![]() 为一条直角边的直角三角形,请直接写出点
为一条直角边的直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.

查看答案和解析>>
科目: 来源: 题型:
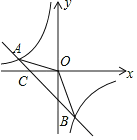
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为![]() 时,问:
时,问:
(1)商场以上的居民住房采光是否有影响,为什么?
(2)若要使商场采光不受影响,两楼应相距多少 米?(结果保留一位小数)
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目: 来源: 题型:
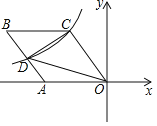
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
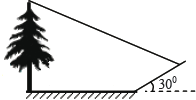
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com