
科目: 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目: 来源: 题型:
【题目】有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=![]() . 若AO=85cm,BO=DO=65cm. 问: 当
. 若AO=85cm,BO=DO=65cm. 问: 当![]() ,较长支撑杆的端点
,较长支撑杆的端点![]() 离地面的高度
离地面的高度![]() 约为_____
约为_____![]() .(参考数据:
.(参考数据:![]()
![]() ,
,![]() .)
.)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为( )
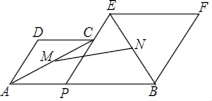
A. ![]() B.
B. ![]() C. 4D. 3
C. 4D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点。
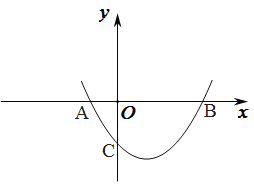
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标
(3)设抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF。
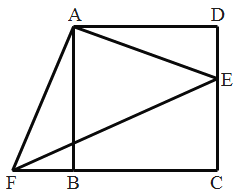
(1)求证:△ADE≌△ABF
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针方向旋转________度得到;
(3)若BC=8,DE=3,求△AEF的面积
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写y与x函数关系式,并求出自变量x的取值范围
(2)当降价多少元时,每星期的利润最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
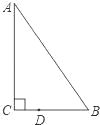
A.70° B.70°或120°
C.120° D.80°
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0), 对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0); ②4a-2b+c>0:③4a+b=0;④当x>-1时,y的值随x值的增大而增大。其中正确的结论有( )
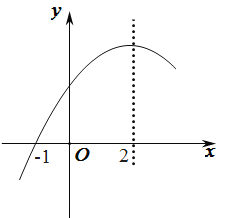
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
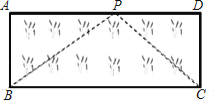
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com