
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,BD为对角线.点P从点B出发,沿线段BA向点A运动,点Q从点D出发,沿线段DB向点B运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到A时,两点都停止.设运动时间为t秒.
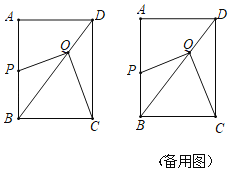
(1)是否存在某一时刻t,使得PQ∥AD?若存在,求出t的值;若不存在,说明理由.
(2)设四边形BPQC的面积为S,求S与t之间的函数关系式.
(3)是否存在某一时刻t,使得S四边形BPQC:S矩形ABCD=9:20?若存在,求出t的值;若不存在,则说明理由.
(4)是否存在某一时刻t,使得PQ⊥CQ?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读资料)
同学们,我们学过用配方法解一元二次方程,也可用配方法求代数式的最值.
(1)求4x2+16x+19的最小值.
解:4x2+16x+19=4x2+16x+16+3=4(x+2)2+3
因(x+2)2大于等于0,所以4x2+16x+19大于等于3,即4x2+16x+19的最小值是3.此时,x=﹣2
(2)求﹣m2﹣m+2的最大值
解:﹣m2﹣m+2=﹣(m2+m)+2=﹣![]()
因![]() 大于等于0,所以﹣
大于等于0,所以﹣![]() 小于等于0,所以﹣
小于等于0,所以﹣![]()
![]()
小于等于![]() ,即﹣m2﹣m+2的最大值是
,即﹣m2﹣m+2的最大值是![]() ,此时,m=﹣
,此时,m=﹣![]() .
.
(探索发现)
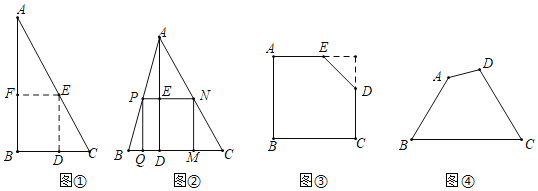
如图①,是一张直角三角形纸片,∠B=90°,AB=8,BC=6,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大.下面给出了未写完的证明,请你阅读下面的证明并写出余下的证明部分,并求出矩形的最大面积与原三角形面积的比值.
解:在AC上任取点E,作ED⊥BC,EF⊥AB,得到矩形BDEF.设EF=x
易证△AEF∽△ACB,则![]() ,
,![]() ,
,![]() ,
,![]() …
…
请你写出剩余部分
(拓展应用)
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),该矩形的面积为 .(直接写出答案)
(实际应用)
如图④,现有一块四边形的木板余料ABCD,经测量AB=70cm,BC=108cm,CD=76cm,且∠B=∠C=60°,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,该矩形的面积为 .(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨2元,月销售量就减少20kg,针对这种水产品情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边AB上一点,延长AD至F使DF=BE,连接CF.
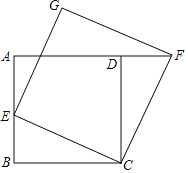
(1)求证:∠BCE=∠DCF;
(2)过点E作EG∥CF,过点F作FG∥CE,问四边形CEGF是什么特殊的四边形,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目: 来源: 题型:
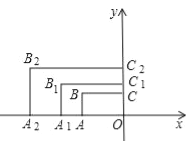
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
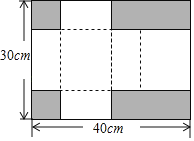
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
查看答案和解析>>
科目: 来源: 题型:
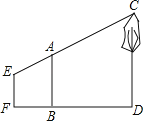
【题目】如图,为了测量一棵树CD的高度,测量者在B处立了一根高为2.5m的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上,若测得BD=7m,FB=3m,EF=1.6m,则树高为_____m.
查看答案和解析>>
科目: 来源: 题型:
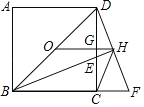
【题目】如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=![]() ;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
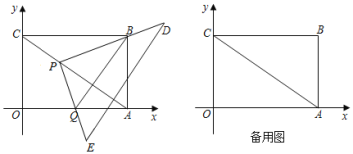
【题目】如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一个直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形顶点B,PE交x轴于点Q
(1)![]() =______;
=______;
(2)在点P从点C运动到点A的过程中,![]() 的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
(3)若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com