
科目: 来源: 题型:
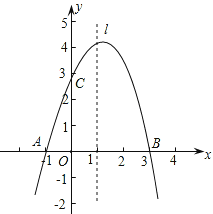
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
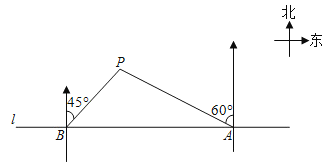
【题目】如图,在一笔直的海岸线L上有A、B两个观测点,A在B的正东方向,AB=2km.有一艘小船在点P处,从A处测得小船在北偏西60°的方向,从B处测得小船在北偏东45°方向.
(1)求P点到海岸线l的距离.
(2)小船从点P处沿射线AP的方向继续行驶,求小船到B处的最短距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 点,与
点,与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,过
两点,过![]() 作
作![]() 垂直于
垂直于![]() 轴于
轴于![]() 点.已知
点.已知![]() .
.
(1)求一次函数![]() 和反比例函数
和反比例函数![]() 的表达式;
的表达式;
(2)观察图象:当![]() 时,比较
时,比较![]() .
.

查看答案和解析>>
科目: 来源: 题型:
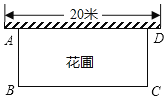
【题目】阿静家在新建的楼房旁围成一个矩形花圃,花圃的一边利用20米长的院墙,另三边用总长为32米的离笆恰好围成.如图,设AB边的长为x米,矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围.
(2)当x为何值时,S有最大值?并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在![]() 中,∠C=90°,AC=8,BC=6,
中,∠C=90°,AC=8,BC=6,
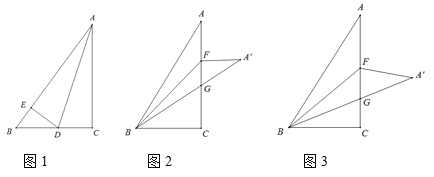
(1)若AD是∠BAC的角平分线,AD交BC边于D,过点D作DE⊥AB与点E(如图1),请求出BE的长及![]() 的值;
的值;
(2)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若BC=CF,如图2,请证明
与AC交于点G,若BC=CF,如图2,请证明![]() ∽
∽![]() ;
;
(3)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若
与AC交于点G,若![]() ,如图3,请求出
,如图3,请求出![]() 的值(可以直接利用第(1)题求出的结论)
的值(可以直接利用第(1)题求出的结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,设二次函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图象经过点(2,6),求函数
的图象经过点(2,6),求函数![]() 的表达式;
的表达式;
(2)若一次函数![]() 的图象与
的图象与![]() 的图象经过x轴上同一点,探究实数
的图象经过x轴上同一点,探究实数![]() ,
,![]() 满足的关系式;
满足的关系式;
(3)已知点![]() 和
和![]() 在函数
在函数![]() 的图象上,若
的图象上,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,连结OD并延长交⊙O于点E,连结AE.
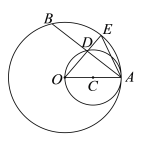
(1)求证:AD=DB.
(2)若AO=10,DE=4,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场拟建三间矩形牛饲养室,饲养室的一面全部靠现有墙(墙长为40m),饲养室之间用一道用建筑材料做的墙隔开(如图).已知计划中的建筑材料可建围墙的总长为60m,设三间饲养室合计长x(m),总占地面积为y(m2).
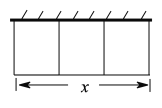
(1)求y关于x的函数表达式和自变量的取值范围.
(2)x为何值时,三间饲养室占地总面积最大?最大为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】小辉和小聪两人在玩转盘游戏时,把一个可以自由转动的转盘A成3等份的扇形区域,把转盘B成2等份的扇形区域,并在每一小区内标上数字(如图所示),游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个区域的数字之和为2的倍数时,则小辉获胜;若指针所指两个区域的数字之和为3的倍数时,则小聪获胜;如果指针落在分割线上,则需重新转动转盘.在这个游戏中,小辉和小聪两人获胜的概率分别为多少?该游戏规则对双方公平吗?
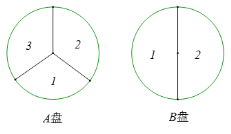
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com