
科目: 来源: 题型:
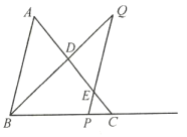
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,把线段
,把线段![]() 沿射线
沿射线![]() 方向平移至
方向平移至![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,又联结
,又联结![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)设![]() ,
,![]() ,试求
,试求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则![]()
=__(结果保留根号).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,用放大镜看△ABC,若边BC的长度变为原来的2倍,那么下列说法中,不正确的是( ).
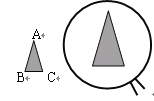
A.边AB的长度也变为原来的2倍;B.∠BAC的度数也变为原来的2倍;
C.△ABC的周长变为原来的2倍;D.△ABC的面积变为原来的4倍;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:正方形ABCD中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
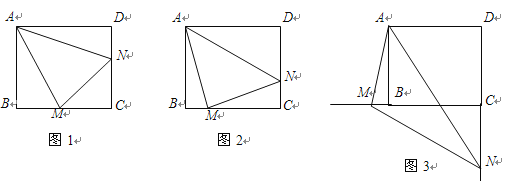
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),求证:
时(如图1),求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),则线段
时(如图2),则线段![]() 和
和![]() 之间数量关系是 ;
之间数量关系是 ;
(3)当![]() 绕点
绕点![]() 旋转到如图3的位置时,猜想线段
旋转到如图3的位置时,猜想线段![]() 和
和![]() 之间又有怎样的的数量关系呢?并对你的猜想加以说明.
之间又有怎样的的数量关系呢?并对你的猜想加以说明.
查看答案和解析>>
科目: 来源: 题型:
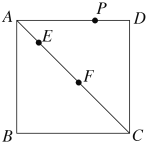
【题目】如图,在正方形![]() 中,
中,![]() 、
、![]() 是对角线
是对角线![]() 上的两个动点,
上的两个动点,![]() 是正方形四边上的任意一点,且
是正方形四边上的任意一点,且![]() ,
,![]() ,设
,设![]() ,当
,当![]() 是等腰三角形时,下列关于
是等腰三角形时,下列关于![]() 点个数的说法中,一定正确的是( )
点个数的说法中,一定正确的是( )
①当![]() (即
(即![]() 、
、![]() 两点重合)时,
两点重合)时,![]() 点有6个;
点有6个;
②当![]() 时,
时,![]() 点最多有9个;
点最多有9个;
③当![]() 是等边三角形时,
是等边三角形时,![]() 点有4个;
点有4个;
④当![]() 点有8个时,
点有8个时,![]() .
.
A.①③B.①④C.②④D.②③
查看答案和解析>>
科目: 来源: 题型:
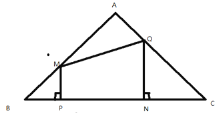
【题目】已知:如图.在△ABC中.AB=AC=5cm,BC=6cm.点P由B出发,沿BC方向匀速运动.速度为1cm/s.同时,点Q从点A出发,沿AC方向匀速运动.速度为1cm/s,过点P作PM![]() BC交AB于点M,过点Q作QN
BC交AB于点M,过点Q作QN![]() BC,垂足为点N,连接MQ,若设运动时间为t(s)(0<t<3),解答下列问题:
BC,垂足为点N,连接MQ,若设运动时间为t(s)(0<t<3),解答下列问题:
(1)当t为何值时,点M是边AB中点?
(2)设四边形PNQM的面积为y(cm2),求出y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PNQM:S△ABC=4:9?若存在,求出此时t的值;若不存在,说明理由;
(4)是否存在某一时刻t,使四边形PNQM为正方形?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题:在1~n(n ≥2)这n个自然数中,每次取两个数(不分顺序),使得所取两数之和大于n,共有多少种取法?
探究:不妨设有m种取法,为了探究m与n的关系,我们先从简单情形入手,再逐次递进,最后猜想得出结论.
探究一:在1~2这2个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于2,有多少种取法?
根据题意,有下列取法:1+2,共1种取法.
所以,当n=2时,m=1.
探究二:在1~3这3个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于3,有多少种取法?
根据题意,有下列取法:1+3,2+3,共2种取法.
所以,当n=3时,m=2.
探究三:在1~4这4个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于4,有多少种取法?
根据题意,有下列取法:1+4,2+4,3+4,2+3,共有3+1=4种取法.
所以,当n=4时,m=3+1=4.
探究四:在1~5这5个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于5,有多少种取法?
根据题意,有下列取法:1+5, 2+5, 3+5, 4+5,2+4,3+4,共有4+2=6种不同的取法.
所以,当n=5时,m=4+2=6.
探究五:在1~6这6个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于6,有多少种不同的取法?(仿照上述探究方法,写出解答过程)
探究六:在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有 种取法?(直接写出结果)
不妨继续探究n=8,9,···时,m与n的关系.
结论:在1~n这n个自然数中,每次取两个数,使得所取的两个数字之和大于n,当n为偶数时,共有___种取法;当n为奇数时,共有___种取法;(只填最简算式)
应用:(1)各边长都是自然数,最大边长为11的不等边三角形共有 个
(2)各边长都是自然数,最大边长为12的三角形共有 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com