
科目: 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
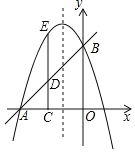
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
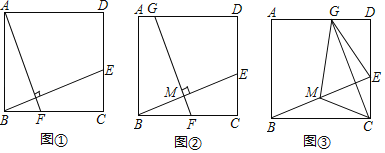
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
(x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
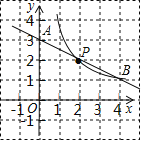
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出一次函数值大于反比例函数值时x的取值范围是: .
(3)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮2人中随机选拔一人当“阳光大课间”领操员,体育老师设计的游戏规则是:将四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.

(1)请用树状图或列表法求出所有可能的结果;
(2)请问这个游戏规则公平吗?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.

查看答案和解析>>
科目: 来源: 题型:
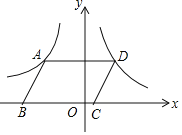
【题目】如图,在平面直角坐标系中,ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣![]() (x<0)与y=
(x<0)与y=![]() (x>0)的图象上,若ABCD的面积为4,则k的值为:_____.
(x>0)的图象上,若ABCD的面积为4,则k的值为:_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
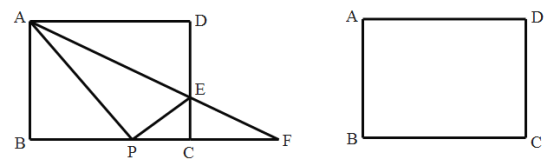
(1)如图,当![]() 在边
在边![]() 上时(点
上时(点![]() 与点
与点![]() 、
、![]() 都不重合),求
都不重合),求![]() 关于
关于![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
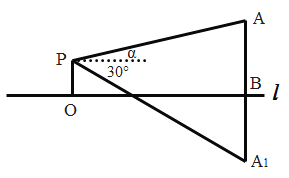
【题目】在湖心有一座小塔,小华想知道这座的高塔的高度,于是他在岸边架起了测角仪,他测量的数据如下(如图所示):测量仪位置![]() 距水平面
距水平面![]() 的距离为1.5米(即
的距离为1.5米(即![]() ),测得塔顶
),测得塔顶![]() 的仰角为
的仰角为![]() (其中
(其中![]() ),测得塔顶在水中倒影
),测得塔顶在水中倒影![]() (即
(即![]() )的俯角为
)的俯角为![]() ,请你根据上述数据求出这座塔的高度(即
,请你根据上述数据求出这座塔的高度(即![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com