
科目: 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目: 来源: 题型:
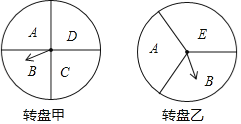
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求DE的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读材料,然后按照要求答题。
阅读材料:为了解方程![]() ,我们可以将
,我们可以将![]() 视为一个整体,然后设
视为一个整体,然后设![]() ,
,![]() ,则原方程可化为:
,则原方程可化为:
![]() ①
①
解得:![]()
当![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴原方程的解为:![]() ,
,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用____________法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )

A. 0.6 B. 0.5 C. 0.45 D. 0.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为![]() .设⊙M与y轴交于D,抛物线的顶点为E.
.设⊙M与y轴交于D,抛物线的顶点为E.
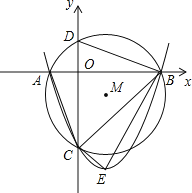
(1)求m的值及抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com