
科目: 来源: 题型:
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“完美四边形”.
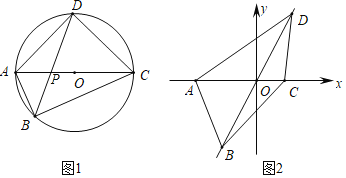
(1)①在“平行四边形、梯形、菱形、正方形”中,一定不是“完美四边形”的有 ;
②若矩形ABCD是“完美四边形”,且AB=4,则BC= ;
(2)如图1,“完美四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“完美四边形”ABCD的四个顶点A(﹣3,0)、C (2,0),B在第三象限,D在第一象限,AC与BD交于点O,直线BD的斜率为![]() ,且四边形ABCD的面积为15
,且四边形ABCD的面积为15![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=a(x﹣h)2+k(a≠0)的图象是抛物线,定义一种变换,先作这条抛物线关于原点对称的抛物线y′,再将得到的对称抛物线y′向上平移m(m>0)个单位,得到新的抛物线ym,我们称ym叫做二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.
(1)已知:二次函数y=2(x+2)2+1,它的顶点关于原点的对称点为 ,这个抛物线的2阶变换的表达式为 .
(2)若二次函数M的6阶变换的关系式为y6′=(x﹣1)2+5.
①二次函数M的函数表达式为 .
②若二次函数M的顶点为点A,与x轴相交的两个交点中左侧交点为点B,在抛物线y6′=(x﹣1)2+5上是否存在点P,使点P与直线AB的距离最短,若存在,求出此时点P的坐标.
(3)抛物线y=﹣3x2﹣6x+1的顶点为点A,与y轴交于点B,该抛物线的m阶变换的顶点为点C.若△ABC是以AB为腰的等腰三角形,请直按写出m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.

(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
(3)若弦CN过△ABC的内心点M,MN=![]() ,求CN.
,求CN.
查看答案和解析>>
科目: 来源: 题型:
【题目】某出租汽车公司计划购买A型和B型两种节能汽车,若购买A型汽车4辆,B型汽车7辆,共需310万元;若购买A型汽车10辆,B型汽车15辆,共需700万元.
(1)A型和B型汽车每辆的价格分别是多少万元?
(2)该公司计划购买A型和B型两种汽车共10辆,费用不超过285万元,且A型汽车的数量少于B型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
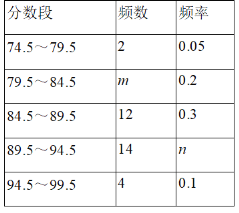
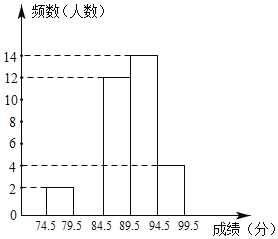
(1)表中m= ,n= ;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,以下结论:①abc>0;②3a+c>0;③m为任意实数,则有a(m2+1)+bm≥0;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2,正确的有( )个.
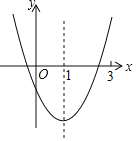
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
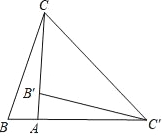
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线过A(1,0)、B(﹣3,0),C(0,﹣3)三点,直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q.
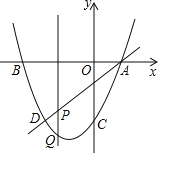
(1)求直线AD及抛物线的解析式;
(2)求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P、Q、D、R为顶点的四边形是平行四边形?若存在,求出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,∠DCE=120°,当∠DCE的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
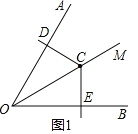
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)由(图1)的位置将∠DCE绕点C逆时针旋转θ角(0<θ<90°),线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com