
科目: 来源: 题型:
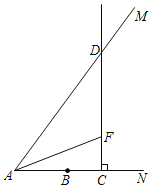
【题目】如图,射线AN上有一点B,AB=5,tan∠MAN=![]() ,点C从点A出发以每秒3个单位长度的速度沿射线AN运动,过点C作CD⊥AN交射线AM于点D,在射线CD上取点F,使得CF=CB,连结AF.设点C的运动时间是t(秒)(t>0).
,点C从点A出发以每秒3个单位长度的速度沿射线AN运动,过点C作CD⊥AN交射线AM于点D,在射线CD上取点F,使得CF=CB,连结AF.设点C的运动时间是t(秒)(t>0).
(1)当点C在点B右侧时,求AD、DF的长.(用含t的代数式表示)
(2)连结BD,设△BCD的面积为S平方单位,求S与t之间的函数关系式.
(3)当△AFD是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
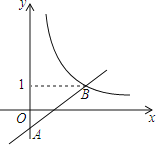
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为推进素质教育,在初一年级设立了六个课外兴趣小组,如图是六个兴趣小组的频数分布直方图和扇形统计图,请根据图中提供的信息回答下列问题:
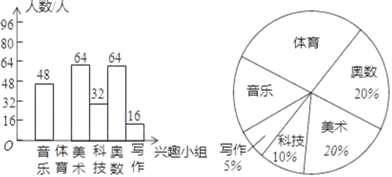
(1)初一年级共有多少人?
(2)补全频数分布直方图.
(3)求“从该年级中任选一名学生,是参加音乐、科技两个小组学生”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目: 来源: 题型:
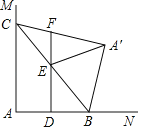
【题目】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
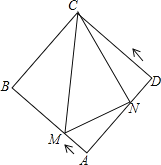
A. 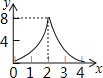 B.
B. 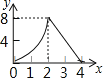
C. 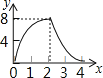 D.
D. 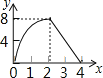
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=﹣x+4与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A,B两点,与x轴的另外一个交点为C
x2+bx+c经过A,B两点,与x轴的另外一个交点为C
(1)填空:b= ,c= ,点C的坐标为 .
(2)如图1,若点P是第一象限抛物线上的点,连接OP交直线AB于点Q,设点P的横坐标为m.PQ与OQ的比值为y,求y与m的数学关系式,并求出PQ与OQ的比值的最大值.
(3)如图2,若点P是第四象限的抛物线上的一点.连接PB与AP,当∠PBA+∠CBO=45°时.求△PBA的面积.
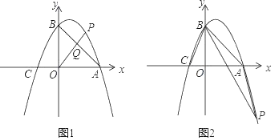
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在△ABC中,AB=5cm,BC=7cm,S△ABC=14cm2,点P从点B出发,以3cm∕s的速度沿边BC向终点C运动,过点P作PQ⊥BC交折线BAC于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
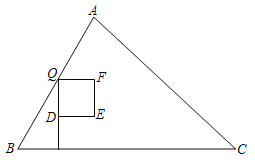
(1)∠C的度数为 ;
(2)当点P不与点C重合,且点F落在边AC上时x的值为 .
(3)当点P不与点B,C重合时,求y关于x的函数解析式;
(4)当直线BD平分△ABC的面积时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com