
科目: 来源: 题型:
【题目】如图,四边形![]() 为正方形,点
为正方形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
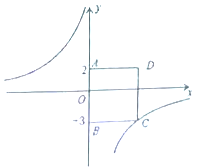
(1)![]() 的线段长为 ;点
的线段长为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)求反比例函数的解析式:
(3)若点![]() 是反比例函数图象上的一点,
是反比例函数图象上的一点,![]() 的面积恰好等于正方形
的面积恰好等于正方形![]() 的面积,求点
的面积,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上的一点,以点
上的一点,以点![]() 为圆心,
为圆心,![]() 为半径的圆弧与
为半径的圆弧与![]() 相切于点
相切于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
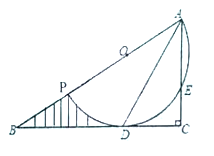
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求圆弧的半径;
,求圆弧的半径;
(3)在![]() 的情况下,若
的情况下,若![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() 和根号)
和根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明袋子中有![]() 个红球,
个红球,![]() 个绿球和
个绿球和![]() 个白球,这些球除颜色外无其他差别,
个白球,这些球除颜色外无其他差别,
![]() 当
当![]() 时,从袋中随机摸出
时,从袋中随机摸出![]() 个球,摸到红球和摸到白球的可能性 (填“相同”或“不相同”);
个球,摸到红球和摸到白球的可能性 (填“相同”或“不相同”);
![]() 从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于
从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于![]() ,则
,则![]() 的值是 ;
的值是 ;
![]() 在
在![]() 的情况下,如果一次摸出两个球,请用树状图或列表法求摸出的两个球颜色不同的概率.
的情况下,如果一次摸出两个球,请用树状图或列表法求摸出的两个球颜色不同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴是x=﹣1,且与x轴交于E点.
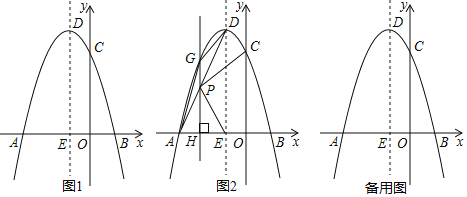
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)如图2,连接AD,设点P是线段AD上的一个动点,过点P作x轴的垂线交抛物线于点G,交x轴于点H,连接AG、GD,当△ADG的面积为1时,
①求点P的坐标;
②连接PC、PE,探究PC、PE的数量关系和位置关系,并说明理由;
(3)设M为抛物线上一动点,N为抛物线的对称轴上一动点,Q为x轴上一动点,当以Q、M、N、E为顶点的四边形为正方形时,请直接写出点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC是等边三角形,点P在射线AC上(点P与点A、点C不重合),点D在线段BC的延长线上,且AP=CD,△PCD′与△PCD关于直线AC对称.
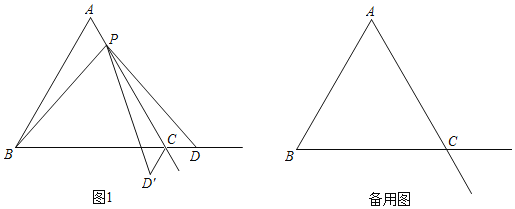
(1)如图1,当点P在线段AC上时,
①求证:PB=PD;
②请求出∠BPD′的度数;
(2)当点P在射线AC上运动时,请直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
(3)将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能否重合?若能重合,请直接写出旋转的角度;若不能重合,请说明理由;
(4)若AB=4,当点P为AC边的中点时,请直接写出PD'的长
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成,长方形OABC的长是12m,宽是4m,按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+2x+c表示.
x2+2x+c表示.
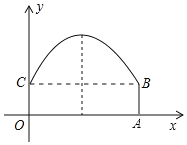
(1)请写出该抛物线的函数关系式;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).

(1)△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;
(2)△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
(3)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算线段OA变换到OA2过程中扫过区域的面积是多少?(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
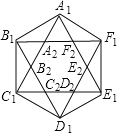
【题目】如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )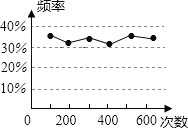
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com