
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.

(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
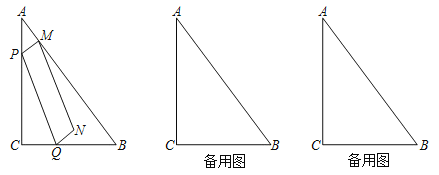
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.
(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;
(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;
(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.
查看答案和解析>>
科目: 来源: 题型:
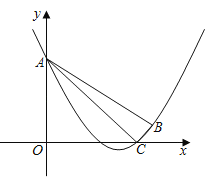
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
科目: 来源: 题型:
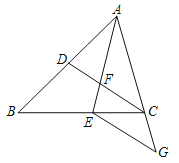
【题目】如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,ABAF=ACAE.
(1)求证:∠AFD=∠AEC;
(2)若EG∥CD,交边AC的延长线于点G,求证:CDCG=FCBD.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
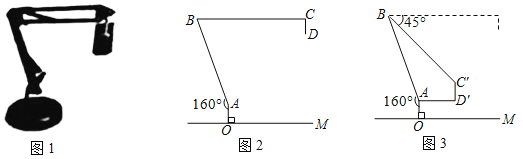
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目: 来源: 题型:
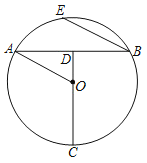
【题目】如图,已知AB是⊙O的弦,点C在⊙O上,且![]() ,联结AO,CO,并延长CO交弦AB于点D,AB=4
,联结AO,CO,并延长CO交弦AB于点D,AB=4![]() ,CD=6.
,CD=6.
(1)求∠OAB的大小;
(2)若点E在⊙O上,BE∥AO,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
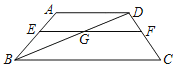
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
查看答案和解析>>
科目: 来源: 题型:
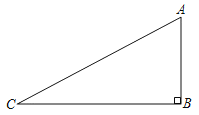
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4,点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果直线l把△ABC分割后的两个部分面积相等,且周长也相等,那么就把直线l叫做△ABC的“完美分割线”,已知在△ABC中,AB=AC,△ABC的一条“完美分割线”为直线l,且直线l平行于BC,若AB=2,则BC的长等于_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果点D、E,F分别在△ABC的边AB、BC,AC上,联结DE、EF,且DE∥AC,那么下列说法错误的是( )
A.如果EF∥AB,那么AF:AC=BD:AB
B.如果AD:AB=CF:AC,那么EF∥AB
C.如果△EFC∽△ABC,那么 EF∥AB
D.如果EF∥AB,那么△EFC∽△BDE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com