
科目: 来源: 题型:
【题目】下面是小飞设计的“过圆外一点作圆的切线”的尺规作图过程.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.

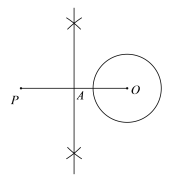
作法:如图,
①连接OP,作线段OP的垂直平分线交OP于点A;
②以点A为圆心,OA的长为半径作圆,交⊙O于B,C两点;
③作直线PB,PC.所以直线PB,PC就是所求作的切线.
根据小飞设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:连接![]() ,
,![]() ,
,
∵![]() 为⊙
为⊙![]() 的直径,
的直径,
∴![]() ( ).
( ).
∴![]() ,
,![]() .
.
∴![]() ,
,![]() 为⊙
为⊙![]() 的切线( ).
的切线( ).
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示. 对于此抛物线有如下四个结论:
,其部分图象如图所示. 对于此抛物线有如下四个结论:
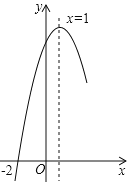
①![]() ;②
;②![]() ;
;
③若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点![]() 不在此抛物线上. 其中正确结论的序号是( )
不在此抛物线上. 其中正确结论的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点A,与
相交于点A,与![]() 轴相交于点B,与
轴相交于点B,与![]() 轴相交于点C,抛物线
轴相交于点C,抛物线![]() 经过点O、点A和点B,已知点A到
经过点O、点A和点B,已知点A到![]() 轴的距离等于2.
轴的距离等于2.
(1)求抛物线的解析式;
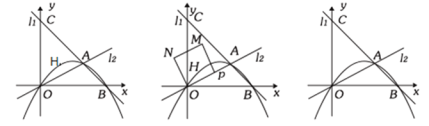
(2)点H为直线![]() 上方抛物线上一动点,当点H到
上方抛物线上一动点,当点H到![]() 的距离最大时,求点H的坐标;
的距离最大时,求点H的坐标;
(3)如图,P为射线OA的一个动点,点P从点O出发,沿着OA方向以每秒![]() 个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
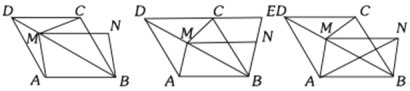
【题目】如图1,在菱形ABCD中,AB=![]() ,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
(1)当∠DCM=30°时,求DM的长度;
(2)如图2,延长BN、DC交于点E,求证:AM·DE=BE·CD;
(3)如图3,连接AN,则AM+AN的最小值是 .
查看答案和解析>>
科目: 来源: 题型:
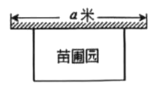
【题目】光明农场准备修建一个矩形苗圃园,苗圃一边靠墙,其他三边用长为48米的篱笆围成.已知墙长为![]() 米.设苗圃园垂直于墙的一边长为
米.设苗圃园垂直于墙的一边长为![]() 米.
米.
(1)求当![]() 为多少米时,苗圃园面积为280平方米;
为多少米时,苗圃园面积为280平方米;
(2)若![]() =22米,当
=22米,当![]() 取何值时,苗圃园的面积最大,并求最大面积.
取何值时,苗圃园的面积最大,并求最大面积.
查看答案和解析>>
科目: 来源: 题型:
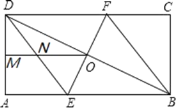
【题目】如图,在矩形ABCD中,过BD的中点O做EF⊥BD,分别与AB、CD交于点E、F.连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若M是AD中点,联结OM与DE交于点N,AD=OM=4,则ON的长是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子中装有1个红球、1个白球和2个蓝球,这些球除颜色外都相同.
(1)从盒子中任意摸出一个球,恰好是白球的概率是 ;
(2)从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,试用树状图或表格列出所以可能的结果,并求两次摸到的球的颜色能配成紫色的概率.(红色和蓝色在一起可配成紫色)
(3)往盒子里面再放入一个白球,如果从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,那么两次摸到的球的颜色能配成紫色的概率是 .
查看答案和解析>>
科目: 来源: 题型:
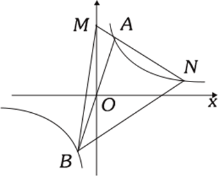
【题目】如图,点A(1,3)为双曲线![]() 上的一点,连接AO并延长与双曲线在第三象限交于点B,M为
上的一点,连接AO并延长与双曲线在第三象限交于点B,M为![]() 轴正半轴一上点,连接MA并延长与双曲线交于点N,连接BM、BN,已知△MBN的面积为
轴正半轴一上点,连接MA并延长与双曲线交于点N,连接BM、BN,已知△MBN的面积为![]() ,则点N的坐标为__________.
,则点N的坐标为__________.
查看答案和解析>>
科目: 来源: 题型:
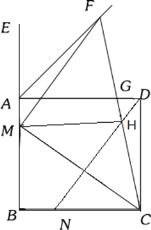
【题目】如图,正方形ABCD中,AB=4,点E是BA延长线上一点,点M、N分别为边AB、BC上的点,且AM=BN=1,连接CM、ND,过点M作MF∥ND与∠EAD的平分线交于点F,连接CF分别与AD、ND交于点G、H,连接MH,则下列结论正确的有( )个
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com