
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
(1)求反比例函数的表达式:
(2)画出直线和双曲线的示意图;
(3)直接写出![]() 的解集______;
的解集______;
(4)若点![]() 是坐标轴负半轴上一点,且满足
是坐标轴负半轴上一点,且满足![]() .直接写出点
.直接写出点![]() 的坐标______.
的坐标______.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.
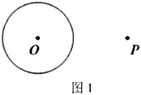
求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
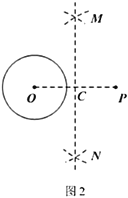
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
科目: 来源: 题型:
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数解析式为( )

A. y=200x B. y=![]() C. y=100x D. y=
C. y=100x D. y=![]()
查看答案和解析>>
科目: 来源: 题型:
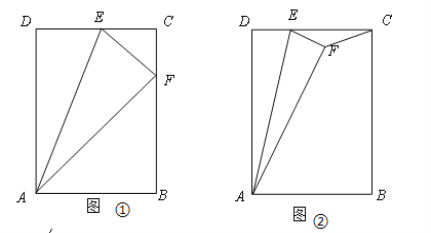
【题目】在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE;
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E、F、C为顶点的三角形是直角三角形,则DE的长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x、月销售量y、月销售利润w(元)的部分对应值如下表:
售价x(元/件) | 40 | 45 |
月销售量y(件) | 300 | 250 |
月销售利润w(元) | 3000 | 3750 |
注:月销售利润=月销售量×(售价-进价)
(1)①求y关于x的函数表达式;
②当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过40元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2400元,则m的值为 .
查看答案和解析>>
科目: 来源: 题型:
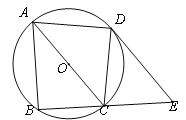
【题目】如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为![]() 的中点,过点D作DE∥AC,交BC的延长线于点E.
的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若CE=![]() ,AB=6,求⊙O的半径.
,AB=6,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
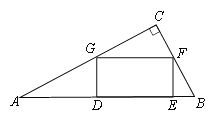
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在边AC、BC上,D、E在边AB上.
(1)求证:△ADG∽△FEB;
(2)若AD=2GD,则△ADG面积与△BEF面积的比为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com