
科目: 来源: 题型:
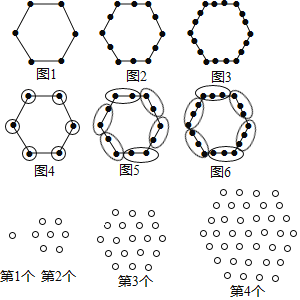
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;……;所以容易求出图10、图n中黑点的个数分别是60、6n.
请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目: 来源: 题型:
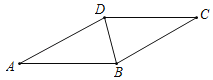
【题目】如图,BD是菱形ABCD的对角线,∠CBD=75°.
(1)求∠A的度数;
(2)请用尺规作图,在AD边上找到一点F,使得∠DBF=45°(不要求写作法,保留作图痕迹)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:t1,t2是方程t2+2t﹣24=0的两个实数根,且t1<t2,抛物线y=![]() x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
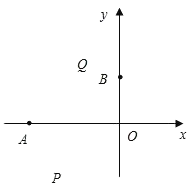
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
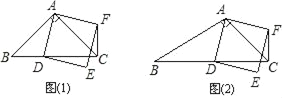
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果超市以每千克6元的价格购进了一批水果,经测算,此水果超市每天需支出固定费用(包括房租,水电费,员工工资等)为600元.若该种水果的销售单价不超过10元,则日销售量为300千克;若该种水果的销售单价超过10元,则每超过1元,日销售就减少12千克.设该种水果的销售单价为x(x>6,且x为整数)元,日净收入为y元(日净收入=日销售利润﹣每天固定支出的费用).
(1)求y与x之间的函数关系式;
(2)此水果超市销售该种水果的日净收入能否达到1560元?否能,请求出此时的销售单价.
查看答案和解析>>
科目: 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com