
科目: 来源: 题型:
【题目】有这样一个问题:探究函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m=_____;
②若M(﹣7,﹣720),N(n,720)为该函数图象上的两点,则n=_____;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,﹣yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y=![]() x﹣1与②中你画出图象的交点的横坐标之和为______.
x﹣1与②中你画出图象的交点的横坐标之和为______.
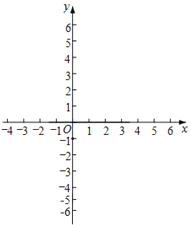
查看答案和解析>>
科目: 来源: 题型:
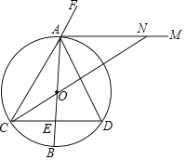
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD外角∠DAF的平分线.
(1)求证:AM是⊙O的切线.
(2)若C是优弧ABD的中点,AD=4,射线CO与AM交于N点,求ON的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为60°”的尺规作图过程
已知:⊙O
求作:矩形ABCD,使得矩形ABCD内接于⊙O,且其对角线AC,BD的夹角为60°.
作法:如图
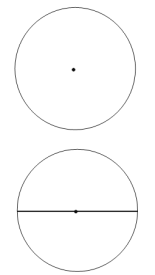
①作⊙O的直径AC;
②以点A为圆心,AO长为半径画弧,交直线AC上方的圆弧于点B;
③连接BO并延长交⊙O于点D;
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点A,C都在⊙O上,
∴OA=OC
同理OB=OD
∴四边形ABCD是平行四边形
∵AC是⊙O的直径,
∴∠ABC=90° ( )(填推理的依据)
∴四边形ABCD是矩形
∵AB= =BO,
∴四边形ABCD四所求作的矩形
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 2 | … |
y | … | ﹣3 | ﹣4 | ﹣3 | 5 | … |
(1)求二次函数的表达式,并写出这个二次函数图象的顶点坐标;
(2)求出该函数图象与x轴的交点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上.
上.
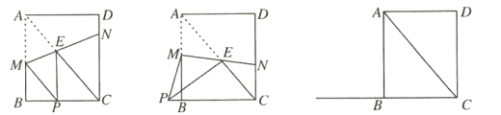
(1)如图1所示,当![]() 时,求
时,求![]() 的长;
的长;
(2)如图2所示,当![]() 时,求
时,求![]() 的长;
的长;
(3)请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
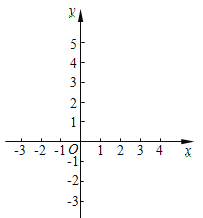
查看答案和解析>>
科目: 来源: 题型:
【题目】小明、小丽两位同学八年级10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:
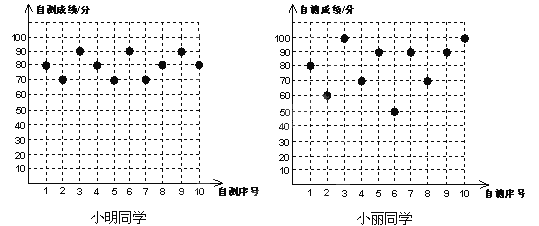
(1)根据上图中提供的数据填写下表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
小明 | 80 | 80 | ||
小丽 | 85 | 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率高的同学是________;
(3)根据图表信息,请你对这两位同学各提一条不超过20个字的学习建议.
查看答案和解析>>
科目: 来源: 题型:
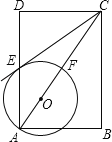
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并说明理由;
(2)若AB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
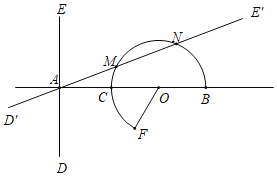
【题目】已知AB⊥DE于A,C,O是AB上一点,且AC=CO=OB=2,以O为圆心作扇形BOF,F到直线AB的距离为![]() .
.
(1)求扇形BOF的面积:
(2)将直线DE绕A点旋转得到直线D'E';
①当直线D'E'与扇形BOF相切时,求旋转角的大小;
②设直线D'E'与扇形BOF的弧相交于M、N,若AM=MN,求MN的长.
查看答案和解析>>
科目: 来源: 题型:
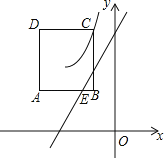
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=![]() (x<0)经过点C.
(x<0)经过点C.
(1)m的取值范围是 ;
(2)若点B(﹣1,1),判断双曲线是否经过点A;
(3)设点B(a,2a+1).
①若双曲线经过点A,求a的值;
②若直线y=2x+2交AB于点E,双曲线与线段AE有交点,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com