
科目: 来源: 题型:
【题目】如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( ).
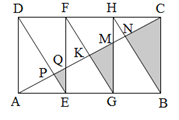
A.6B.8
C.10D.12
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 与点
与点![]() .
.
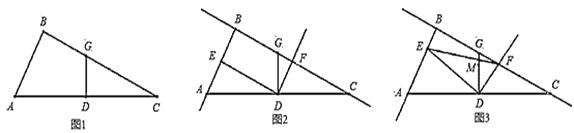
(1)求![]() 的长.
的长.
(2)如图2,![]() 点为射线
点为射线![]() 上一动点,连接
上一动点,连接![]() ,线段
,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交直线
交直线![]() 与点
与点![]() .
.
①若![]() 时,求
时,求![]() 的长:
的长:
②如图3,连接![]() 交直线
交直线![]() 与点
与点![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]()
(1)无论![]() 取任何实数,方程总有实数根吗?试做出判断并证明你的结论.
取任何实数,方程总有实数根吗?试做出判断并证明你的结论.
(2)抛物线![]() 的图象与
的图象与![]() 轴两个交点的横坐标均为整数,且
轴两个交点的横坐标均为整数,且![]() 也为正整数.若
也为正整数.若![]() ,
,![]() 是此抛物线上的两点,且
是此抛物线上的两点,且![]() ,请结合函数图象确定实数
,请结合函数图象确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
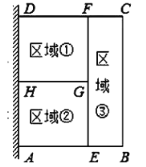
【题目】因2019年下半年猪肉大涨,某养猪专业户想扩大养猪场地,但为了节省材料,利用一面墙(墙足够长)为一边,用总长为120![]() 的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设
的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设![]() 的长度为
的长度为![]() (
(![]() ),矩形区域
),矩形区域![]() 的面积
的面积![]() (
(![]() ).
).
(1)求![]() 与
与![]() 之间的函数表达式,并注明自变量
之间的函数表达式,并注明自变量![]() 的取值范围.
的取值范围.
(2)当![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() .(1)已知点
.(1)已知点![]() 在第一象限的抛物线上,则点
在第一象限的抛物线上,则点![]() 的坐标是_______.(2)在(l)的条件下连接
的坐标是_______.(2)在(l)的条件下连接![]() ,
,![]() 为抛物线上一点且
为抛物线上一点且![]()
![]() ,则点
,则点![]() 的坐标是_______.
的坐标是_______.

查看答案和解析>>
科目: 来源: 题型:
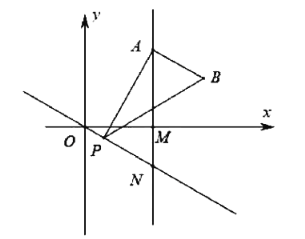
【题目】如图,已知点![]() 是第一象限内横坐标为2的一个定点,
是第一象限内横坐标为2的一个定点,![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 点不变,
点不变,![]() 点随之运动,当点
点随之运动,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 运动的路径长是( )
运动的路径长是( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
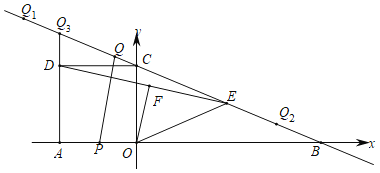
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
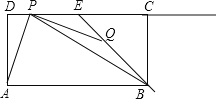
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
(元) | 19 | 20 | 21 | 30 |
(件) | 62 | 60 | 58 | 40 |
(1)根据表中数据的规律,分别写出毎日销售量y(件),每日的利润w(元)关于销售单价x(元)之间的函数表达式.(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?
(3)根据物价局规定,这种纪念品的销售单价不得高于32元,如果公司要获得每日不低于350元的利润,那么制造这种纪念花灯每日的最低制造成本需要多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com