
科目: 来源: 题型:
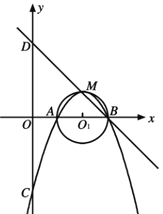
【题目】如图,半径为1的![]() 与
与![]() 轴交于
轴交于![]() 两点,圆心
两点,圆心![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数的解析式.
(2)经过坐标原点![]() 的直线
的直线![]() 与
与![]() 相切,求直线
相切,求直线![]() 的解析式.
的解析式.
(3)试问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:

(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出
四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出![]() 厂家的合格率为
厂家的合格率为![]() ,并根据检测数据绘制了两幅不完整的统计图.
,并根据检测数据绘制了两幅不完整的统计图.
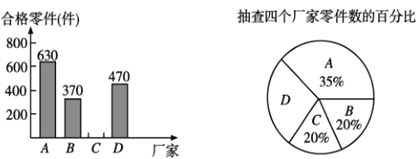
(1)抽查![]() 厂家的零件为______件,扇形统计图中
厂家的零件为______件,扇形统计图中![]() 厂家对应的圆心角为______.
厂家对应的圆心角为______.
(2)抽查![]() 厂家的合格零件为_______件.
厂家的合格零件为_______件.
(3)若要从![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出
四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出![]() ,
,![]() 两个厂家同时被选中的概率,并列出所有等可能的结果.
两个厂家同时被选中的概率,并列出所有等可能的结果.
查看答案和解析>>
科目: 来源: 题型:
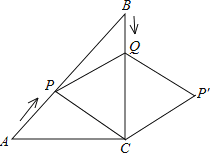
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目: 来源: 题型:
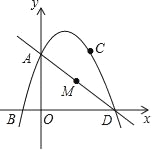
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.

查看答案和解析>>
科目: 来源: 题型:
【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
查看答案和解析>>
科目: 来源: 题型:
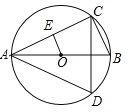
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
求:(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com