
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(![]() ,3),B(
,3),B(![]() ,2),C(0,
,2),C(0,![]() ).
).
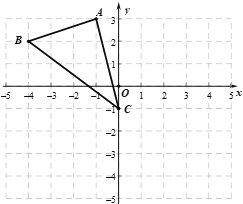
(1)以y轴为对称轴,把△ABC沿y轴翻折,画出翻折后的△![]() ;
;
(2)在(1)的基础上,
①以点C为旋转中心,把△![]() 顺时针旋转90°,画出旋转后的△
顺时针旋转90°,画出旋转后的△![]() ;
;
②点![]() 的坐标为 ,在旋转过程中点
的坐标为 ,在旋转过程中点![]() 经过的路径
经过的路径![]() 的长度为_____(结果保留π).
的长度为_____(结果保留π).
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小华同学设计的“作三角形的高线”的尺规作图的过程.
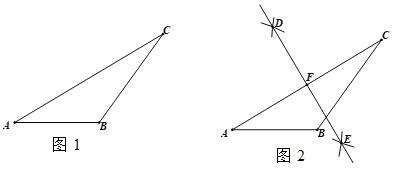
已知:如图1,△ABC.
求作:AB边上的高线.
作法:如图2,
①分别以A,C为圆心,大于![]() 长
长
为半径作弧,两弧分别交于点D,E;
② 作直线DE,交AC于点F;
③ 以点F为圆心,FA长为半径作圆,交AB的延长线于点M;
④ 连接CM.
则CM 为所求AB边上的高线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接DA,DC,EA,EC,
∵由作图可知DA=DC =EA=EC,
∴DE是线段AC的垂直平分线.
∴FA=FC .
∴AC是⊙F的直径.
∴∠AMC=______°(___________________________________)(填依据),
∴CM⊥AB.
即CM就是AB边上的高线.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于点A(2,a).
交于点A(2,a).
(1)求![]() 与
与![]() 的值;
的值;
(2)画出双曲线![]() 的示意图;
的示意图;
(3)设点![]() 是双曲线
是双曲线![]() 上一点(
上一点(![]() 与
与![]() 不重合),直线
不重合),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,结合图象,直接写出
时,结合图象,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
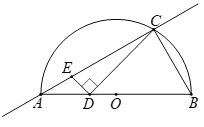
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
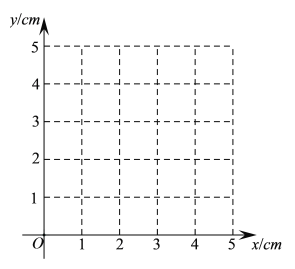
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为P,且与y轴交于点A,与直线
的顶点为P,且与y轴交于点A,与直线![]() 交于点B,C(点B在点C的左侧).
交于点B,C(点B在点C的左侧).

(1)求抛物线![]() 的顶点P的坐标(用含a的代数式表示);
的顶点P的坐标(用含a的代数式表示);
(2)横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
①当![]() 时,请直接写出“W区域”内的整点个数;
时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠MON=60°,OF平分∠MON,点A在射线OM上, P,Q是射线ON上的两动点,点P在点Q的左侧,且PQ=OA,作线段OQ的垂直平分线,分别交OM,OF,ON于点D,B,C,连接AB,PB.


(1)依题意补全图形;
(2)判断线段 AB,PB之间的数量关系,并证明;
(3)连接AP,设![]() ,当P和Q两点都在射线ON上移动时,
,当P和Q两点都在射线ON上移动时,![]() 是否存在最小值?若存在,请直接写出
是否存在最小值?若存在,请直接写出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“永定楼”,作为门头沟区的地标性建筑,因其坐落在永定河畔而得名.为测得其高度,低空无人机在A处,测得楼顶端B的仰角为30°,楼底端C的俯角为45°,此时低空无人机到地面的垂直距离AE为23![]() 米,那么永定楼的高度BC是______米(结果保留根号).
米,那么永定楼的高度BC是______米(结果保留根号).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是_______(填序号).
①抛一枚质地均匀的硬币,落地时结果“正面朝上”;
②在“石头,剪刀,布”的游戏中,小明随机出的是剪刀;
③四张一样的卡片,分别标有数字1,2,3,4,从中随机
取出一张,数字是1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com