
科目: 来源: 题型:
【题目】鲜丰水果店计划用![]() 元/盒的进价购进一款水果礼盒以备销售.
元/盒的进价购进一款水果礼盒以备销售.
![]() 据调查,当该种水果礼盒的售价为
据调查,当该种水果礼盒的售价为![]() 元/盒时,月销量为
元/盒时,月销量为![]() 盒,每盒售价每增长
盒,每盒售价每增长![]() 元,月销量就相应减少
元,月销量就相应减少![]() 盒,若使水果礼盒的月销量不低于
盒,若使水果礼盒的月销量不低于![]() 盒,每盒售价应不高于多少元?
盒,每盒售价应不高于多少元?
![]() 在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了
在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了![]() ,而每盒水果礼盒的售价比(1)中最高售价减少了
,而每盒水果礼盒的售价比(1)中最高售价减少了![]() ,月销量比(1)中最低月销量
,月销量比(1)中最低月销量![]() 盒增加了
盒增加了![]() ,结果该月水果店销售该水果礼盒的利润达到了
,结果该月水果店销售该水果礼盒的利润达到了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】在新的教学改革的推动下,某中学初年级积极推进英语小班教学.为了了解一段时间以来的英语小班教学的学习效果,年级组织了多次定时测试,现随机选取甲,乙两个班,从中各抽取20名同学在某一次定时测试中的英语成绩,过程如下,请补充完整
收集数据:
甲班的20名同学的英语成绩统计(单位:分)
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计(满分为100分)(单位:分)
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
数量分数/ 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据:
请回答下列问题:
(1)完成下表:
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a= |
乙班 | 80.35 | b= | 78 |
甲班成绩得分扇形图(x表示分数)

(2)在班成绩行分的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数 ,c= .
(3)根据以上数据,你认为 班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是: ;
(4)若英语定时成绩不低于80分为优秀,请估计全年级1600人中优秀人数为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】临近端午,某超市准备购进某品牌的白粽、豆沙粽、蛋黄粽,三种品种的粽子共1000袋(每袋均为同一品种的粽子),其中白粽每袋12个,豆沙粽每袋8个,蛋黄粽每袋6个.为了推广,超市还计划将三个品种的粽子各取![]() 出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的
出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的![]() ,则豆沙粽最多购进__袋.
,则豆沙粽最多购进__袋.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人同时骑自行车分别从A、B两地出发到AB之间的C地,且A、B、C三地在同一直线上.当乙到达C地时甲还未到达,乙在C地等了5分钟,接到甲的电话说他的自行车坏了需要工具修理,于是乙在C地拿了工具箱立即以原来![]() 倍的速度前往甲坏车处,乙与甲会合后帮助甲花了10分钟修好自行车,然后两人以甲原来
倍的速度前往甲坏车处,乙与甲会合后帮助甲花了10分钟修好自行车,然后两人以甲原来![]() 倍的速度骑行同时到达C地.甲乙两人距C地的距离之和y(米)与甲所用时间x(分钟)之间的函数关系如图所示(乙接电话和找工具箱的时间忽略不计),则A、B两地之间的距离为___米.
倍的速度骑行同时到达C地.甲乙两人距C地的距离之和y(米)与甲所用时间x(分钟)之间的函数关系如图所示(乙接电话和找工具箱的时间忽略不计),则A、B两地之间的距离为___米.

查看答案和解析>>
科目: 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A. B.
B.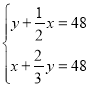 C.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线;C1:y=﹣![]() (x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.

(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).
(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;
(2)若过原点的两条直线OA、OB分别与二次函数y=![]() x2交于点A(m,
x2交于点A(m,![]() m2)和点B(n,
m2)和点B(n,![]() n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
n2)(mn<0)且OA⊥OB,试求直线AB上的定点;
(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C的点,且DE2=DBDA,延长AE至F,使得AE=EF,设BF=5,cos∠BED=![]() .
.
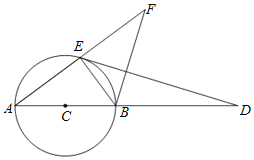
(1)求证:△DEB∽△DAE;
(2)求DA、DE的长;
(3)若点F在B、E、M三点确定的圆上,求MD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com