
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,3),抛物线G:y=x2-2x+c(c为常数)的顶点坐标为M,其对称轴与x轴相交于点N.
(1)若抛物线G经过点A,求出其解析式,并写出点M的坐标.
(2)若点B(x1,y1)和点C(x1+3,y2)在抛物线G上,试比较y1,y2的大小.
(3)连接OM,若45°≤∠MON≤60°,请直接写出c的取值范围.

查看答案和解析>>
科目: 来源: 题型:
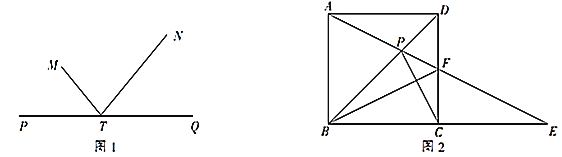
【题目】如图1,直线PQ的同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点M,N为关于直线PQ的衍射点.如图2,BD是矩形ABCD的对角线,E是边BC延长线上的一点,且CE=BC,连接AE交CD于点F,交BD于点P,连接BF,CP.
(1)求证:点A,B是关于直线CD的衍射点.
(2)若点C,F是关于直线BD的衍射点,CP=2PF=2![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,及时推广生态文明建设,某校组织全校师生参与植树节活动.为调査栽种的柳树的成活情况,对全校学生的植树情况进行了抽样调查,并将调查结果分为“A.优良”“B.合格”C.差”三类.
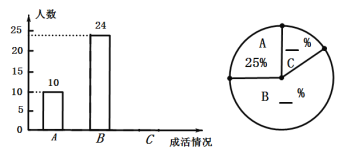
请根据图中信息,解答下列问题.
(1)求被调查学生的人数.
(2)将上面的条形统计图与扇形统计图补充完整.
(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人),A类1棵,B类2棵,C类1棵,该小组恰好有两棵树被抽査,求恰好是两棵B类树被抽查的概率.
查看答案和解析>>
科目: 来源: 题型:
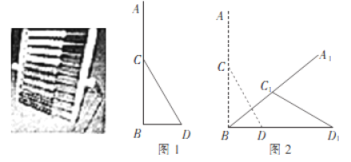
【题目】如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据:![]() ≈1.732,
≈1.732, ![]() ≈4.583,π≈3.142)
≈4.583,π≈3.142)
查看答案和解析>>
科目: 来源: 题型:
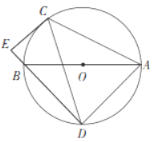
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E.
(1)连接AC、AD,求证:∠DAC+∠ACE=180°.
(2)若∠ABD=2∠BDC,求证:CE是⊙O的切线.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?
查看答案和解析>>
科目: 来源: 题型:
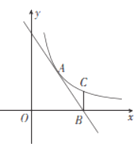
【题目】如图,反比例函数y=![]() (x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
(x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的是某地区今年4月份的囗平均气温的频数分布直方图(直方图中每一组数都包括前一个边界值,不包括后一个边界值),则下列结论中错误的是( )

A.该地区4月份的口平均气温在18℃以上(含18℃)的共有10天
B.该直方图的组距是4℃
C.该地区4月份的口平均气温的最大值至少是22℃
D.该直方图中口平均气温为6~10℃的这一组数的频数为3,频率为0.1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l1:y=6x+6与x轴、y轴分别交于A、D两点,直线l2:y=﹣x+3与x轴、y轴分别交于B、C两点.
(1)在直线l2上找一点E,使|AE﹣DE|的值最大,并求|AE﹣DE|的最大值.
(2)以AB为边作矩形ABMN,点C在边MN上,动点P从B出发,沿射线BM方向移动,作△PAB关于直线PA的对称△PAB'.是否存在点P,使得△PMB'是直角三角形?若存在,请直接写出所有符合题意的点P的坐标?若不存在,请说明理由.
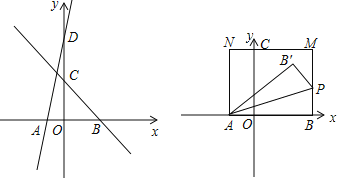
查看答案和解析>>
科目: 来源: 题型:
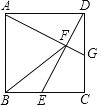
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)若BC=4,求AG的长;
(2)连接BF,求证:AB=FB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com