
科目: 来源: 题型:
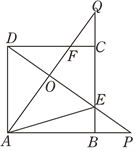
【题目】如图,四边形ABCD是正方形,点P,Q分别在边AB,BC的延长线上且BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②△OAE∽△OPA;③当正方形的边长为3,BP=1时,cos∠DFO=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目: 来源: 题型:
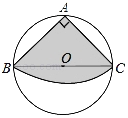
【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为![]() ,则这块圆形纸片的直径为( )
,则这块圆形纸片的直径为( )
A. 12cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目: 来源: 题型:
【题目】从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组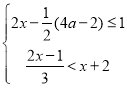 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )
=1有非负整数解的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 为线段
为线段![]() 中点.
中点.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)以抛物线的顶点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 是圆上一动点,点
是圆上一动点,点![]() 为
为![]() 的中点(如图2);
的中点(如图2);
①当![]() 面积最大时,求
面积最大时,求![]() 的长度;
的长度;
②若点![]() 为
为![]() 的中点,求点
的中点,求点![]() 运动的路径长.
运动的路径长.
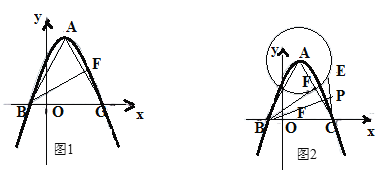
查看答案和解析>>
科目: 来源: 题型:
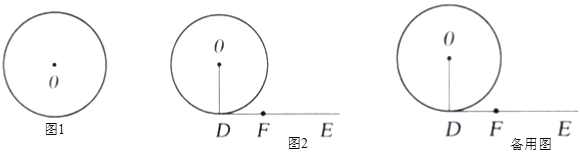
【题目】(1)①如图1,请用直尺(不带刻度)和圆规作出![]() 的内接正三角形
的内接正三角形![]() (按要求作图,不要求写作法,但要保留作图痕迹).
(按要求作图,不要求写作法,但要保留作图痕迹).
②若![]() 的内接正三角形
的内接正三角形![]() 边长为6,求
边长为6,求![]() 的半径;
的半径;
(2)如图2,![]() 的半径就是(1)中所求半径的值.点
的半径就是(1)中所求半径的值.点![]() 在
在![]() 上,
上,![]() 是
是![]() 的切线,点
的切线,点![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,点
方向移动,点![]() 是
是![]() 上的点(不与点
上的点(不与点![]() 重合),
重合),![]() 是
是![]() 的切线.设点
的切线.设点![]() 运动的时间为
运动的时间为![]() (秒),当
(秒),当![]() 为何值时,
为何值时,![]() 是直角三角形,请你求出满足条件的所有
是直角三角形,请你求出满足条件的所有![]() 值.
值.
查看答案和解析>>
科目: 来源: 题型:
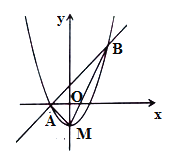
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,且抛物线与直线
,且抛物线与直线![]() 相交于
相交于![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(1)![]() ,
,![]() ,
,![]() (直接写出结果);
(直接写出结果);
(2)当![]() 时,则
时,则![]() 的取值范围为 (直接写出结果);
的取值范围为 (直接写出结果);
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使得
,使得![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的最大面积及点
的最大面积及点![]() 坐标.
坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明代表学校参加“我和我的祖国”主题宣传教育活动,该活动分为两个阶段,第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目(依次用![]() 、
、![]() 、
、![]() 表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用
表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用![]() 、
、![]() 表示),参加人员在每个阶段各随机抽取一个项目完成.
表示),参加人员在每个阶段各随机抽取一个项目完成.
(1)用画树状图或列表的方法,列出小明参加项目的所有等可能的结果;
(2)求小明恰好抽中![]() 、
、![]() 两个项目的概率.
两个项目的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,可计算出甲的平均成绩是 环(直接写出结果);
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,根据计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com