
科目: 来源: 题型:
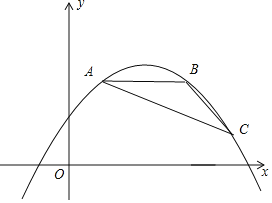
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
查看答案和解析>>
科目: 来源: 题型:
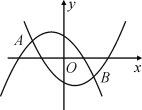
【题目】已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当a=![]() 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线l,l1,l2都垂直于x轴,l1,l2分别经过A,B两点,l在直线l1,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
查看答案和解析>>
科目: 来源: 题型:
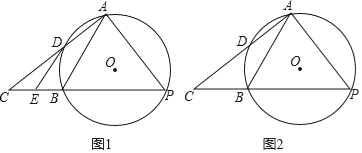
【题目】已知AB是⊙O的弦,点P是优弧AB上的一个动点,连接AP,过点A作AP的垂线,交PB的延长线于点C.
(1)如图1,AC与⊙O相交于点D,过点D作⊙O的切线,交PC于点E,若DE∥AB,求证:PA=PB;
(2)如图2,已知⊙O的半径为2,AB=2![]() .
.
①当点P在优弧AB上运动时,∠C的度数为 °;
②当点P在优弧AB上运动时,△ABP的面积随之变化,求△ABP面积的最大值;
③当点P在优弧AB上运动时,△ABC的面积随之变化,△ABC的面积的最大值为 .
查看答案和解析>>
科目: 来源: 题型:
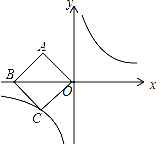
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
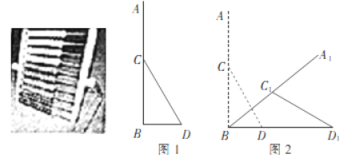
【题目】如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据:![]() ≈1.732,
≈1.732, ![]() ≈4.583,π≈3.142)
≈4.583,π≈3.142)
查看答案和解析>>
科目: 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37 34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38 34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
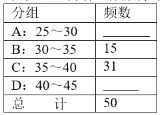
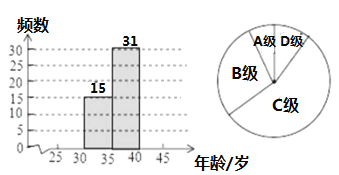
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为 ;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目: 来源: 题型:
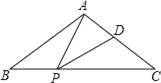
【题目】如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com