
科目: 来源: 题型:
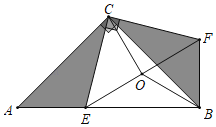
【题目】如图,等腰Rt△ABC,AB=6,点E是斜边AB上的一点(端点A、B除外),将△CAE绕C逆时针旋转90°至△CBF,连接EF,且EF的中点为O,连OB、OC,设AE=x,
(1)求证:OB=OC;
(2)用x表示△BEF的面积S△BEF,并求S△BEF的最大值;
(3)用x表示四边形BECF的周长C,并求C的最小值.
查看答案和解析>>
科目: 来源: 题型:
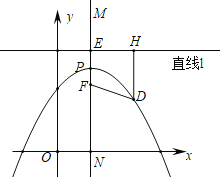
【题目】寻找神奇点!每条抛物线内都有一个神奇的点F(也叫焦点),还有一条与之配套的直线!(也叫准线),使得抛物线上的每个点到F的距离等于到直线l的距离.如图,对于抛物线上任意一点D,都有DF=DH.
根据以上知识,我们来完成以下问题:
(1)因为抛物线是轴对称图形,由对称性可知这个神奇的点F应在抛物线的 上,且准线l一定与对称轴垂直即l⊥MN(对称轴).
(2)若准线l与对称轴MN交于E,MN交抛物线于点P,则PE、PF的数量关系是PE PF(填>、=、<),
(3)求抛物线y=﹣(x﹣2)2+4的神奇点(焦点)F的坐标.
查看答案和解析>>
科目: 来源: 题型:
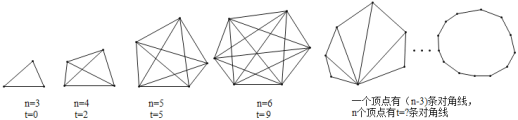
【题目】如图,先研究下面三角形、四边形、五边形、六边形…多边形的边数n及其对角线条数t的关系,再完成下面问题:
(1)若一个多边形是七边形,它的对角线条数为 ,n边形的对角线条数为t= (用n表示).
(2)求正好65条对角线的多边形是几边形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=(1﹣m)x2﹣mx﹣1与x轴交于A、B两点,顶点为P.
(1)求m的取值范围;
(2)若A、B位于原点两侧,求m的取值范围;
(3)若顶点P在第四象限,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
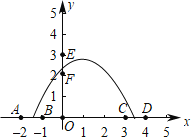
【题目】如图,在一个与地面垂直的截面中建立直角坐标系(横坐标表示地面位移,纵坐标表示高度),一架无人机的飞行路线为y=ax2+bx+c(a≠0),在直角坐标系中x轴上的线段AB上的某点起飞,途经空中线段EF上的某点,最后在线段CD上的某点降落,其中A(﹣2,0)、B(﹣1,0)、C(3,0)、D(4,0)、E(0,3)、F(0,2),则下列结论正确的有_____(填序号)
(1)abc<0;
(2)从起飞到当x≤1时无人机一直是上升的;
(3)2≤a+b+c≤4.5;
(4)最大飞行高度不超过4.
查看答案和解析>>
科目: 来源: 题型:
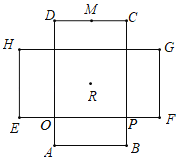
【题目】如图,将一个8cm×16cm智屏手机抽象成一个矩形ABCD,其中AB=8cm,AD=16cm,现将正在竖屏看视频的这个手机围绕它的中心R顺时针旋转90°后改为横屏看视频,其中,M是CD的中点,则图中等于45°的角有_____个.(按图中所标字母写出符合条件的角)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,每次旋转都以图中的A、B、C、D、E、F中不同的点为旋转中心,旋转角度为k90°(k为整数),现在要将左边的阴影四边形正好通过n次旋转得到右边的阴影四边形,则n的值可以是( )
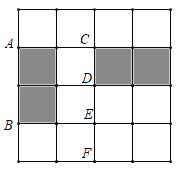
A.n=1可以,n=2,3不可B.n=2可以,n=1,3不可
C.n=1,2可以,n=3不可D.n=1,2,3均可
查看答案和解析>>
科目: 来源: 题型:
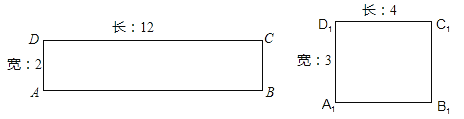
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图矩形![]() 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1)是某公园里的一种健身器材,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com