
科目: 来源: 题型:
【题目】为积极响应党和国家精准扶贫战略计划,某公司在农村租用了 720亩闲置土地种植了乔 木型、小乔木型和灌木型三种茶树. 为达到最佳种植收益,要求种植乔木型茶树的面积是小乔木型茶树面积的2倍,灌木型茶树的面积不得超过乔木型茶树面积的![]() 倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年重庆国际马拉松赛于3月31日在南滨公园鸣枪开跑已知A、B两补给站之间的路程为1470米,志愿者甲、乙都从A站出发支援B站.甲先出发,且在途中停留了4分钟,甲出发6分钟后,乙才从A站出发.在整个行走过程中,两人保持各自速度匀速行走,两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达B站时,甲与B站相距的路程是_____米.

查看答案和解析>>
科目: 来源: 题型:
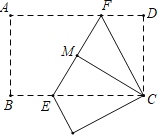
【题目】如图,把一张矩形纸片折叠,点A与点C重合,折痕为EF,再将△CDF沿CF折叠,点D恰好落在EF上的点M处,若BC=6厘米,则EF的长为_____厘米.
查看答案和解析>>
科目: 来源: 题型:
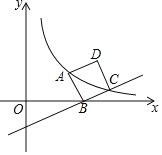
【题目】如图,正方形ABCD的顶点B在x轴上,点A、点C在双曲线y=![]() (k>0,x>0)上.若直线BC的解析式为y=
(k>0,x>0)上.若直线BC的解析式为y=![]() x﹣2,则k的值为( )
x﹣2,则k的值为( )
A.24B.12C.6D.4
查看答案和解析>>
科目: 来源: 题型:
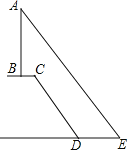
【题目】国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52°≈0.79,tan52°≈1.28)( )
A.28米B.29.6米C.36.6米D.57.6米
查看答案和解析>>
科目: 来源: 题型:
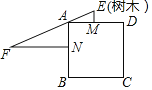
【题目】《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF过点A,且ME=30步,NF=750步,则正方形的边长为( )
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒2个单位长的速度向点
轴以每秒2个单位长的速度向点![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时停止运动,设点
时停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒.将线段
秒.将线段![]() 的中点绕点
的中点绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得点
得点![]() ,点
,点![]() 随点
随点![]() 的运动而运动,连接
的运动而运动,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
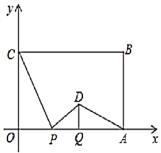
(1)求证:![]() ∽
∽![]() ;
;
(2)请用含![]() 的代数式表示出点
的代数式表示出点![]() 的坐标;
的坐标;
(3)求![]() 为何值时,
为何值时,![]() 的面积最大,最大为多少?
的面积最大,最大为多少?
(4)在点![]() 从
从![]() 向
向![]() 运动的过程中,点
运动的过程中,点![]() 与点
与点![]() 所在的直线能否平分矩形
所在的直线能否平分矩形![]() 的面积?若能,求
的面积?若能,求![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
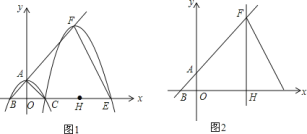
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴正半轴上),
轴正半轴上),![]() 为等腰直角三角形,且面积为
为等腰直角三角形,且面积为![]() ,现将抛物线沿
,现将抛物线沿![]() 方向平移,平移后的抛物线过点
方向平移,平移后的抛物线过点![]() 时,与
时,与![]() 轴的另一点为
轴的另一点为![]() ,其顶点为
,其顶点为![]() ,对称轴与
,对称轴与![]() 轴的交点为
轴的交点为![]() .
.
![]() 求
求![]() 、
、![]() 的值.
的值.
![]() 连接
连接![]() ,试判断
,试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
![]() 现将一足够大的三角板的直角顶点
现将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.
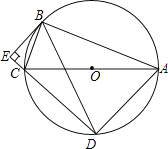
(1)求证:CB是∠ECA的角平分线;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com