
科目: 来源: 题型:
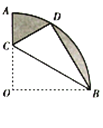
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,![]() ;
;
(3)是否存在点P,使△PAD是直角三角形,若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的销售价p(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示设第x天的日销售额为w(单位:元)
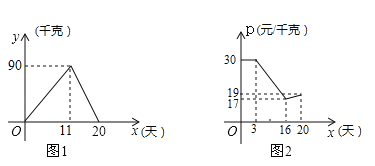
(1)第11天的日销售额w为 元;
(2)观察图象,求当16≤x≤20时,日销售额w与上市时间x之间的函数关系式及w的最大值;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的销售价p元千克将批发来的草莓全部售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
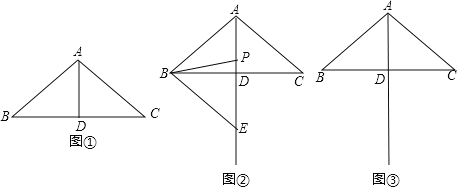
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.

(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
查看答案和解析>>
科目: 来源: 题型:
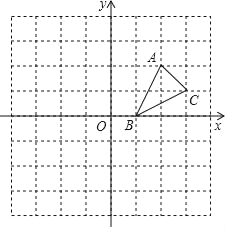
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
查看答案和解析>>
科目: 来源: 题型:
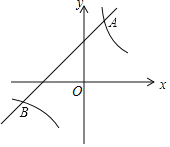
【题目】如图,一次函数y1=x+2的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.

查看答案和解析>>
科目: 来源: 题型:
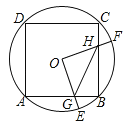
【题目】(2016湖北省咸宁市)如图,边长为4的正方形ABCD内接于点O,点E是![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
①![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为![]() .
.
其中正确的是________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )

A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com