
科目: 来源: 题型:
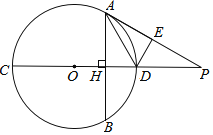
【题目】如图,CD为⊙O的直径,弦AB垂直于CD,垂足为H,∠EAD=∠HAD.
(1)求证:AE为⊙O的切线;
(2)延长AE与CD的延长线交于点P,过D 作DE⊥AP,垂足为E,已知PA=2,PD=1,求⊙O的半径和DE的长.
查看答案和解析>>
科目: 来源: 题型:
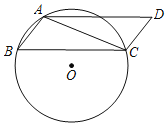
【题目】操作、证明:如图,在平行四边形ABCD中,连接AC,以点C为圆心BC为半径画弧,交△ABC的外接圆O于点E,连接AE、CE.
(1)求证:AD=CE,∠D=∠E.
(2)连接CO,求证:CO平分∠BCE.
(3)判断:“一组对边相等且一组对角相等的四边形是平行四边形”是 命题(填“真”或“假”).
查看答案和解析>>
科目: 来源: 题型:
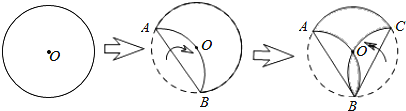
【题目】如图,将半径为3的圆形纸片,按顺序折叠两次,折叠后的弧AB和弧BC都经过圆心O.
(1)连接OA、OB,求证:∠AOB=120°;
(2)图中阴影部分的面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读小明用下面的方法求出方程2![]() ﹣3x=0的
﹣3x=0的
解法1:令 原方程化为2t﹣3t2=0 解方程2t﹣3t2=0,得t1=0,t2= 所以 将方程 得x=0或 经检验,x=0或 所以,原方程的解是x=0或 | 解法2:移项,得2 方程两边同时平方,得4x=9x2, 解方程4x=9x2,得x=0或 经检验,x=0或 所以,原方程的解是x=0或 |
请仿照他的某一种方法,求出方法x﹣![]() =﹣1的解.
=﹣1的解.
查看答案和解析>>
科目: 来源: 题型:
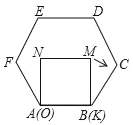
【题目】已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,顶点
中,顶点![]() 是它们的公共顶点,
是它们的公共顶点,![]() ,
,![]() .
.
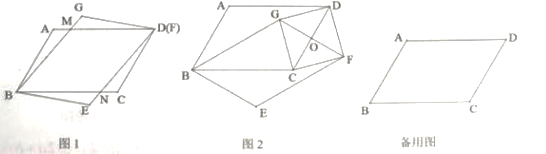
(特例感悟)(1)当顶点![]() 与顶点
与顶点![]() 重合时(如图1),
重合时(如图1),![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(探索论证)(2)如图2,当![]() 时,四边形
时,四边形![]() 是什么特殊四边形?试证明你的结论;
是什么特殊四边形?试证明你的结论;
(拓展应用)(3)试探究:当![]() 等于多少度时,以点
等于多少度时,以点![]() 为顶点的四边形是矩形?请给予证明.
为顶点的四边形是矩形?请给予证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数).
是常数).
(1)当![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() ,函数值
,函数值![]() 时,以之对应的自变量
时,以之对应的自变量![]() 的值只有一个,求
的值只有一个,求![]() 的值;
的值;
(3)当![]() ,自变量
,自变量![]() 时,函数有最小值为-10,求此时二次函数的表达式.
时,函数有最小值为-10,求此时二次函数的表达式.
查看答案和解析>>
科目: 来源: 题型:
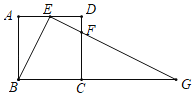
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
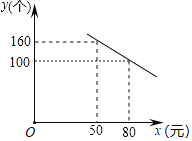
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com