
科目: 来源: 题型:
【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
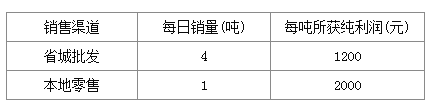
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙0的直径,AB=10,CD是⊙0的切线,C为切点,交直线AB于E,AD⊥CD于D,AD=2CD.
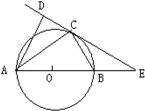
(1)求证:∠CAB=∠CAD;
(2)求CD的长;
(3)求AE的长.
查看答案和解析>>
科目: 来源: 题型:
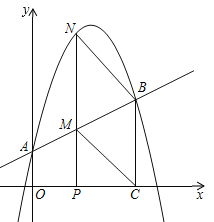
【题目】如图,抛物线![]() 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
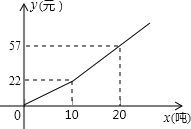
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△AB.C内接于⊙0,点D在半径OB的延长线上,∠BCD=∠A=30°.
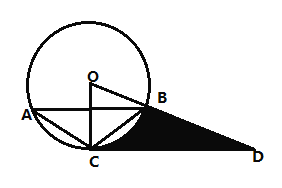
(1)判断直线CD与⊙0的位置关系,并说明理由
(2)若⊙0的半径为1,求阴影部分面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.

查看答案和解析>>
科目: 来源: 题型:
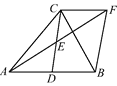
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:

(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,抛物线
,抛物线![]() 经过两点
经过两点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() .
.
(1)求抛物线的解析式;
(2)如图1,过点![]() 作
作![]() 轴,交抛物线于另一点
轴,交抛物线于另一点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度在线段
个单位长度的速度在线段![]() 上由点
上由点![]() 向点
向点![]() 运动(点
运动(点![]() 不与点
不与点![]() 和点
和点![]() 重合),设运动时间为
重合),设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 轴右侧的抛物线与点
轴右侧的抛物线与点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,正方形![]() ,边
,边![]() 在
在![]() 轴上,点
轴上,点![]() 与点
与点![]() 重合,边长
重合,边长![]() 为
为![]() 个单位长度,将正方形
个单位长度,将正方形![]() 沿射线
沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度平移,时间为
个单位长度的速度平移,时间为![]() 秒,在平移过程中,请写出正方形
秒,在平移过程中,请写出正方形![]() 的边恰好与抛物线有两个交点时
的边恰好与抛物线有两个交点时![]() 的取值范围.
的取值范围.
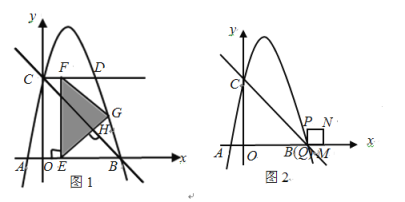
查看答案和解析>>
科目: 来源: 题型:
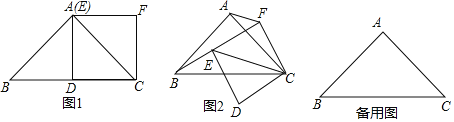
【题目】(1)如图1,在![]() 中,
中,![]() 90°,点
90°,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 恰好与点
恰好与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)在(1)的条件下,如果正方形![]() 绕点
绕点![]() 旋转,连接
旋转,连接![]() ,
,
①线段![]() 与
与![]() 的数量关系有无变化?请仅就图2的情形给出证明;
的数量关系有无变化?请仅就图2的情形给出证明;
②当正方形![]() 旋转到
旋转到![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com