
科目: 来源: 题型:
【题目】已知:抛物线y=ax2﹣3(a﹣1)x+2a﹣6(a>0).
(1)求证:抛物线与x轴有两个交点.
(2)设抛物线与x轴的两个交点的横坐标分别为x1,x2(其中x1>x2).若t是关于a的函数、且t=ax2﹣x1,求这个函数的表达式;
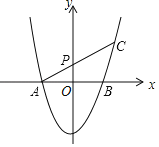
(3)若a=1,将抛物线向上平移一个单位后与x轴交于点A、B.平移后如图所示,过A作直线AC,分别交y的正半轴于点P和抛物线于点C,且OP=1.M是线段AC上一动点,求2MB+MC的最小值.
查看答案和解析>>
科目: 来源: 题型:
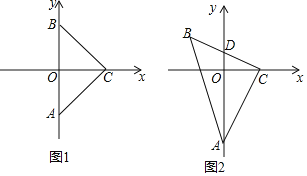
【题目】如图,△ABC在平面直角坐标系中,∠ACB=90°,AC=BC,A的坐标是(0,m)(m<0),点C的坐标是(2,0),点B在x轴上方.
(1)如图1所示,若点B在y轴上,则m的值是 ;
(2)如图2所示,BC与y轴交于点D.
①若m=﹣6,求点B的坐标;
②若y轴恰好平分∠BAC,求OD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
查看答案和解析>>
科目: 来源: 题型:
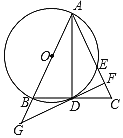
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=![]() ,CF=2,求DF和BG的长.
,CF=2,求DF和BG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,将矩形ABCD折叠,使点C与点A重合,点D落在点G处,折痕为EF.
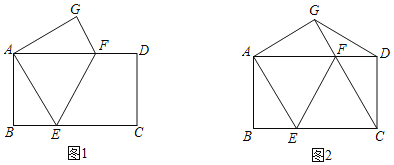
(1)如图1,求证:BE=GF;
(2)如图2,连接CF、DG,若CE=2BE,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形都为等腰三角形
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目: 来源: 题型:
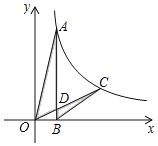
【题目】如图,已知点A,点C在反比例函数y=![]() (k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
(k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )

A.2mB.4mC.![]() mD.
mD.![]() m
m
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com