
科目: 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球,请用树状图或列表法求下列事件的概率.
(1)两次取出的小球的标号相同;
(2)两次取出的小球标号的和等于6.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中的两个图形
中的两个图形![]() 与
与![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为图形
为图形![]() 上任意一点,如果
上任意一点,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 间的“和睦距离”,记作
间的“和睦距离”,记作![]() ,若图形
,若图形![]() 有公共点,则
有公共点,则![]() .
.
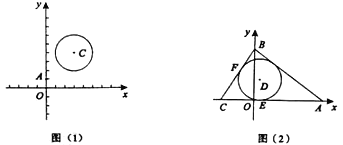
(1)如图(1),![]() ,
,![]() ,⊙
,⊙![]() 的半径为2,则
的半径为2,则![]() ,
,![]() ;
;
(2)如图(2),已知![]() 的一边
的一边![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() .
.
①![]() 是
是![]() 内一点,若
内一点,若![]() 、
、![]() 分别且⊙
分别且⊙![]() 于E、F,且
于E、F,且![]() ,判断
,判断![]() 与⊙
与⊙![]() 的位置关系,并求出
的位置关系,并求出![]() 点的坐标;
点的坐标;
②若以![]() 为半径,①中的
为半径,①中的![]() 为圆心的⊙
为圆心的⊙![]() ,有
,有![]() ,
,![]() ,直接写出
,直接写出![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产并销售某种产品,整理出该商品在第![]() (
(![]() )天的售价
)天的售价![]() 与
与![]() 函数关系如图所示,已知该商品的进价为每件30元,第
函数关系如图所示,已知该商品的进价为每件30元,第![]() 天的销售量为
天的销售量为![]() 件.
件.
(1)试求出售价![]() 与
与![]() 之间的函数关系是;
之间的函数关系是;
(2)请求出该商品在销售过程中的最大利润;
(3)在该商品销售过程中,试求出利润不低于3600元的![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
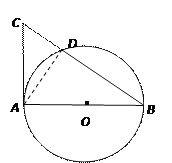
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.

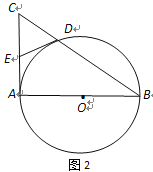
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.

∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.
点睛:考查解直角三角形,圆周角定理,切线的判定与性质等,属于圆的综合题,比较基础.注意切线的证明方法,是高频考点.
【题型】解答题
【结束】
21
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程![]() 的两个根;
的两个根;
(2)若方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
(3)若抛物线与直线![]() 相交于
相交于![]() ,
,![]() 两点,写出抛物线在直线下方时
两点,写出抛物线在直线下方时![]() 的取值范围.
的取值范围.
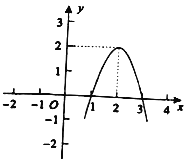
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若![]() ,则称点D是△ABC中BC边上的“好点”.
,则称点D是△ABC中BC边上的“好点”.
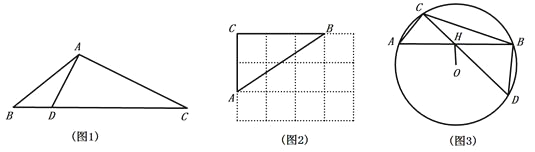
(1)如图2,△ABC的顶点是![]() 网格图的格点,请仅用直尺画出AB边上的一个“好点”.
网格图的格点,请仅用直尺画出AB边上的一个“好点”.
(2)△ABC中,BC=9,![]() ,
,![]() ,点D是BC边上的“好点”,求线段BD的长.
,点D是BC边上的“好点”,求线段BD的长.
(3)如图3,△ABC是![]() 的内接三角形,OH⊥AB于点H,连结CH并延长交
的内接三角形,OH⊥AB于点H,连结CH并延长交![]() 于点D.
于点D.
①求证:点H是△BCD中CD边上的“好点”.
②若![]() 的半径为9,∠ABD=90°,OH=6,请直接写出
的半径为9,∠ABD=90°,OH=6,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
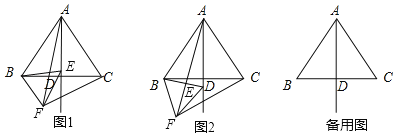
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com