
科目: 来源: 题型:
【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
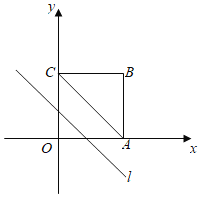
A. B.
B.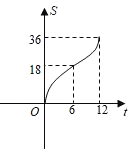
C.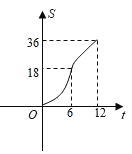 D.
D.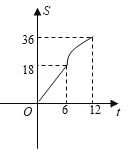
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )

A.6B.2![]() +1C.
+1C.![]() D.9
D.9
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=![]() ,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;
(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);
(3)如果AG=8,求DE的长.
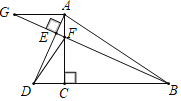
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C (0,3),点P在该抛物线的对称轴上,且纵坐标为2![]() .
.
(1)求抛物线的表达式以及点P的坐标;
(2)当三角形中一个内角α是另一个内角β的两倍时,我们称α为此三角形的“特征角”.
①当D在射线AP上,如果∠DAB为△ABD的特征角,求点D的坐标;
②点E为第一象限内抛物线上一点,点F在x轴上,CE⊥EF,如果∠CEF为△ECF的特征角,求点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.
(1)求证:BD2=DEAD;
(2)如果∠ABC=∠DCE,求证:BDCE=BEDE.
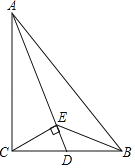
查看答案和解析>>
科目: 来源: 题型:
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
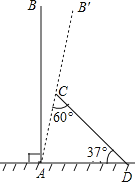
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,将抛物线C1:y=x2﹣2x向左平移2个单位,向下平移3个单位得到新抛物线C2.
(1)求新抛物线C2的表达式;
(2)如图,将△OAB沿x轴向左平移得到△O′A′B′,点A(0,5)的对应点A′落在平移后的新抛物线C2上,求点B与其对应点B′的距离.
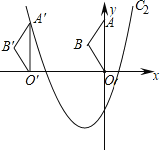
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向上平移3个单位长度,画出平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕B1逆时针旋转90°,画出旋转后的△A2B1C2,求线段B1C1旋转过程中扫过的面积(结果保留π).

查看答案和解析>>
科目: 来源: 题型:
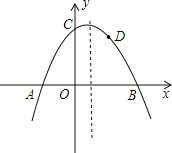
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
注:二次函数![]() (
(![]() ≠0)的对称轴是直线
≠0)的对称轴是直线![]() =
=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com