
科目: 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,抛物线y=﹣![]() x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),点C是抛物线的顶点,且⊙C与y轴相切,点P为⊙C上一动点.若点D为PA的中点,连结OD,则OD的最大值是( )
x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),点C是抛物线的顶点,且⊙C与y轴相切,点P为⊙C上一动点.若点D为PA的中点,连结OD,则OD的最大值是( )

A.![]() B.
B.![]() C.2
C.2![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是( )
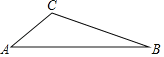
A.0<CP≤1B.0<CP≤2C.1≤CP<8D.2≤CP<8
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,书中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深2寸(ED=2寸),锯道长8寸”,问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算圆形木材的直径AC是( )
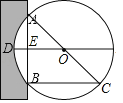
A.5寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD(AB>AD)中,点M是边DC上的一点,点P是射线CB上的动点,连接AM,AP,且∠DAP=2∠AMD.
(1)若∠APC=76°,则∠DAM= ;
(2)猜想∠APC与∠DAM的数量关系为 ,并进行证明;
(3)如图1,若点M为DC的中点,求证:2AD=BP+AP;
(4)如图2,当∠AMP=∠APM时,若CP=15,![]() =
=![]() 时,则线段MC的长为 .
时,则线段MC的长为 .

查看答案和解析>>
科目: 来源: 题型:
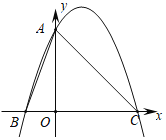
【题目】如图,对称轴为直线x=1的抛物线与x轴交于B、C两点,与y轴交于点A(0,3),且OA=OC.
(1)求抛物线的解析式;
(2)点P是直线AC上方抛物线上的一点,过点P作PD⊥x轴于点D.若△PDC与△AOB相似,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是半圆的直径,O为圆心,点C是弧BE的中点,过点C作PC⊥AE于点D,交AB的延长线于点P
(1)求证:直线PC是⊙O的切线;
(2)若∠P=30°,AD=3,求阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.
(1)1辆A型货车和1辆B型货车的满载量分别是多少?
(2)该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?
查看答案和解析>>
科目: 来源: 题型:
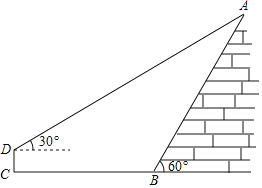
【题目】如图,为了拆除震后危楼,抗震减灾工作组对所剩部分危楼楼房进行摸排测量.在危楼楼角B点处,测得危楼楼顶A的仰角为60°;沿楼角B点的正前方前进8米到达点C,在离C点2米高的D处测得危楼楼顶A的仰角为30°.请根据以上测量数据,求出楼顶A离地面的高度.(![]() ≈1.7,精确到1米)
≈1.7,精确到1米)
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网的不断发展,移动支付的普及率越来越高,人们在购物时可选择的付款方式越来越多样化.为了解人们购物时常用付款方式,在某步行街进行了随机抽样调查,根据调查结果绘制以下两幅不完整统计图,请结合图中所给信息解答下列问题:
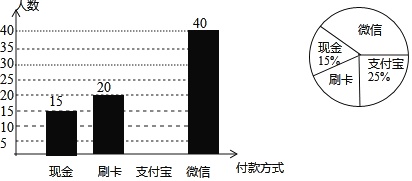
(1)此次共调查了 人,表示常用“微信”付款方式的扇形圆心角度数为 ,并补全条形统计图.
(2)该步行街某天的人流量约为2.4万人,其中约有50%的人参与购物,根据调查获得的信息,估计在这一天购物时用“微信”付款方式的人数为多少万人?
(3)若甲、乙两人在购物时,选择“现金”、“刷卡”、“支付宝”、“微信”(分别用A、B、C、D表示)付款的可能性相同.请通过列表或画树形图的方法,求两人在购物时,用同一种付款方式的概率.
查看答案和解析>>
科目: 来源: 题型:
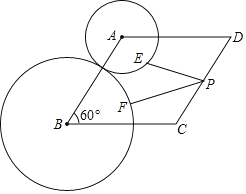
【题目】已知菱形ABCD中,AB=5,∠B=60°,⊙A的半径为2,⊙B的半径为3,点E、F分别为⊙A、⊙B上的动点,点P为DC边上的动点,则PE+PF的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com