
科目: 来源: 题型:
【题目】制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃,煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是26 ℃.
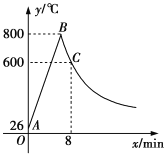
(1)分别求出材料煅烧和锻造时y关于x的函数解析式,并写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作,那么锻造的操作时间有多长?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
查看答案和解析>>
科目: 来源: 题型:
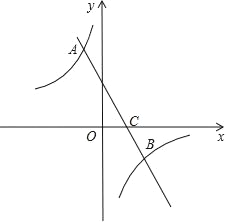
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了保护生态环境,某工厂在一段时间内限产并投入资金进行治污改造.如图描述的是月利润y(万元)和月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )

A.5月份该厂的月利润最低
B.治污改造完成后,每月利润比前一个月增加30万元
C.治污改造前后,共有6个月的月利润不超过120万元
D.治污改造完成后的第8个月,该厂月利润达到300万元
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
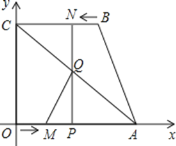
(1) 求![]() 的面积
的面积![]() 与运动时间
与运动时间![]() 的函数关系式, 并写出自变量
的函数关系式, 并写出自变量![]() 的取值范围, 当
的取值范围, 当![]() 为何值时,
为何值时,![]() 的值最大?
的值最大?
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(3) 当![]() 为以
为以![]() 为底的等腰三角形时,求
为底的等腰三角形时,求![]() 值.
值.
(4) 是否存在这样的![]() 值,使直线
值,使直线![]() 将
将![]() 的周长和面积同时平分?若存在,求出
的周长和面积同时平分?若存在,求出![]() 值,若不存在,说明理由.
值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:因为直线![]() ,其中
,其中![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为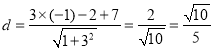 .
.
根据以上材料,解答下列问题:
(1)点![]() 到直线
到直线![]() 的距离;
的距离;
(2)已知![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() 为2,判断
为2,判断![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(3)已知直线![]() 与
与![]() 平行,
平行,![]() 、
、![]() 是直线
是直线![]() 上的两点且
上的两点且![]() ,
,![]() 是直线
是直线![]() 上任意一点,求
上任意一点,求![]() 的面积.
的面积.
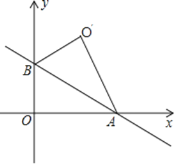
(4)如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,把
两点,把![]() 沿直线
沿直线![]() 翻折后得到
翻折后得到![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
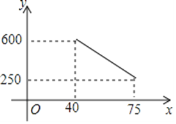
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为![]() (元),求每月获得利润
(元),求每月获得利润![]() (元)关于销售单价
(元)关于销售单价![]() (元)的函数解析式;
(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量).
查看答案和解析>>
科目: 来源: 题型:
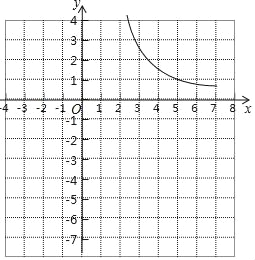
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com