
科目: 来源: 题型:
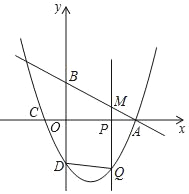
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目: 来源: 题型:
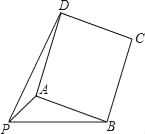
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
科目: 来源: 题型:
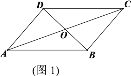
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分):
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表
年级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
七年级 | 98 | 94 | a | m | 7.6 |
八年级 | 98 | n | 94 | 93 | 6.6 |
根据以上信息,完成下列问题
(1)填空:a= ;m= ;n= ;
(2)两个年级中, 年级成绩更稳定;
(3)七年级两名最高分选手分别记为:A1,A2,八年级第一、第二名选手分别记为B1,B2,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
查看答案和解析>>
科目: 来源: 题型:
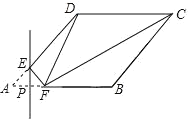
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
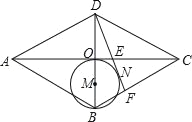
A. 3B. 4C. 4.8D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( )
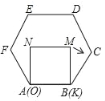
A. 0.5B. 0.7C. ![]() ﹣1D.
﹣1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
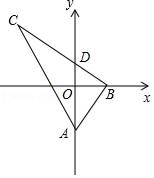
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com