
科目: 来源: 题型:
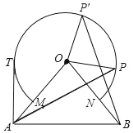
【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧![]() 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与圆弧相切,求AT的长.
(3)Q为优弧上一点,当△AOQ面积最大时,请直接写出∠BOQ的度数为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】有A、B、C1、C2四张同样规格的硬纸片,它们的背面完全一样,正面如图1所示.将它们背面朝上洗匀后,随机抽取并拼图.
(1)填空:随机抽出一张,正面图形正好是中心对称图形的概率是__________.
(2)随机抽出两张(不放回),其图形可拼成如图2的四种图案之一.请你用画树状图或列表的方法,分析拼成哪种图案的概率最大?

查看答案和解析>>
科目: 来源: 题型:
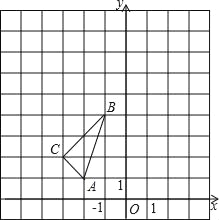
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将Rt△ABC平移到△A′B′C′的位置,其中∠C=90°,使得点C′与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的周长为( )
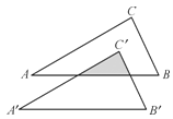
A.5B.6C.7D.8
查看答案和解析>>
科目: 来源: 题型:
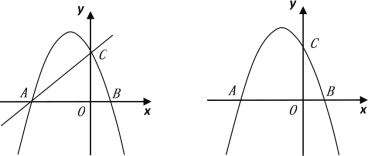
【题目】如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.
(1)求A、B、C的坐标;
(2)过抛物线上一点F作y轴的平行线,与直线AC交于点G.若FG=![]() AC,求点F的坐标;
AC,求点F的坐标;
(3)E(0,﹣2),连接BE.将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′,O、B、E的对应点分别为O′、B′、E′.若点B′、E′两点恰好落在抛物线上,求点B′的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:将△ABD绕点A逆时针旋转60°得到△ACE,可得AE=AD, CE=BD,∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则 ∠ACE+∠ACD=180°,易知△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
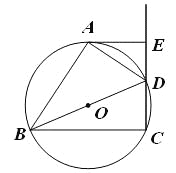
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
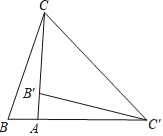
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com