
科目: 来源: 题型:
【题目】材料1:在设计人体雕塑时,存在一个分隔点,使雕塑的上部(腰以上)与下部(腰以下)之比,等于下部与全部(全身)之比,可以增加视觉美观,数学上把这个点叫“黄金分割点”. 为了研究这个点,我们在线段AB上取点C(如图1),点C把AB分成AC和CB两段,其中BC是较小的一段,现要使![]() 即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入
即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入![]() ,即
,即![]() ,也即x2+x-1=0,解之得,
,也即x2+x-1=0,解之得,![]() .所以
.所以![]() =
=![]() ,人们把
,人们把![]() 这个数叫黄金分割数,点C叫“黄金分割点”.
这个数叫黄金分割数,点C叫“黄金分割点”.
材料2:由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果![]() ,那么称直线l为该图形的“黄金分割线”.
,那么称直线l为该图形的“黄金分割线”.
(1)如图2,点C是线段AB的黄金分割点(AC>CB),取线段AB的中点O,作点C关于点O的对称点![]() ,则
,则![]() ;继续取线段AC的中点
;继续取线段AC的中点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,试猜想点
,试猜想点![]() 是否线段A
是否线段A![]() 的黄金分割点,若是,请证明,若不是,请说明理由;
的黄金分割点,若是,请证明,若不是,请说明理由;
(2)如图3,在平面直角坐标系中, A(-![]() ,0),B(1,0),C(4-
,0),B(1,0),C(4-![]() ,2),求△ABC中经过点C的“黄金分割线”解析式.
,2),求△ABC中经过点C的“黄金分割线”解析式.
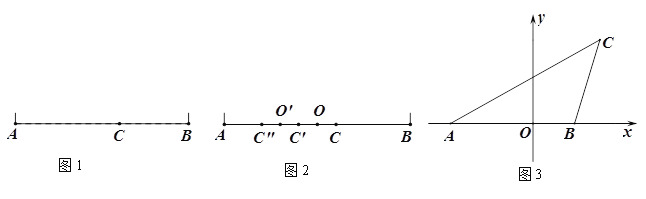
查看答案和解析>>
科目: 来源: 题型:
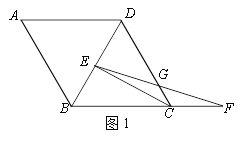
【题目】等腰△ABD中,AD=BD,将△ABD绕腰BD的中点顺时针旋转180°,得到△CDB,CE平分∠BCD交BD于点E,在BC的延长线上取点F,使CF=DE,连接EF交CD于点G.
(1)如图1,∠A=60°,AB=4,求CF的长;
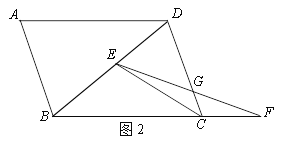
(2)如图2,求证:DE=2CG.
查看答案和解析>>
科目: 来源: 题型:
【题目】某批发城在冬天到来之际进了一批保暖衣,男生的保暖衣每件价格60元,女生的保暖衣每件价格40元,第一批共购买100件.
(1)第一批购买的保暖衣的总费用不超过5400元,求女生保暖衣最少购买多少件?
(2)第二批购买保暖衣,购买男、女生保暖衣的件数比为![]() ,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了
,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了![]() 元 ,女生保暖衣的价格比第一批购买的价格上每件增加了
元 ,女生保暖衣的价格比第一批购买的价格上每件增加了![]() 元,男生保暖衣的数量比第二批增加了
元,男生保暖衣的数量比第二批增加了![]() ,女生保暖衣的数量比第二批减少了
,女生保暖衣的数量比第二批减少了![]() ,第二批与第三批购买保暖衣的总费用相同,求
,第二批与第三批购买保暖衣的总费用相同,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】毕业典礼的开幕式上需要采购花店的鲜花.花店提供甲、乙两种造型的花束数量若干,甲种花束由4枝红花、1枝黄花和1枝紫花搭配而成,乙种花束由4枝黄花和2枝紫花搭配而成.已知每枝红花、黄花和紫花的成本之比是3:2:1,甲、乙两种造型的花束数量之比是2:9.甲、乙两种花束成本价分别为每种造型的三种鲜花的成本之和,甲种花束的销售利润率是20%,乙种花束的销售利润率为10%,这次买卖,花店获得的利润率是___________.
查看答案和解析>>
科目: 来源: 题型:
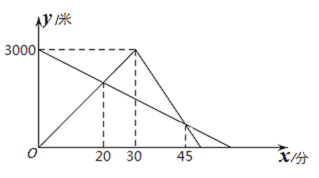
【题目】某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要____________分到达A地.
查看答案和解析>>
科目: 来源: 题型:
【题目】有![]() 两个口袋,
两个口袋,![]() 口袋中装有两个分别标有数字2,3的小球,
口袋中装有两个分别标有数字2,3的小球,![]() 口袋中装有三个分别标有数字
口袋中装有三个分别标有数字![]() 的小球(每个小球质量、大小、材质均相同).小明先从
的小球(每个小球质量、大小、材质均相同).小明先从![]() 口袋中随机取出一个小球,用
口袋中随机取出一个小球,用![]() 表示所取球上的数字;再从
表示所取球上的数字;再从![]() 口袋中顺次取出两个小球,用
口袋中顺次取出两个小球,用![]() 表示所取两个小球上的数字之和.
表示所取两个小球上的数字之和.
(1)用树状图法或列表法表示小明所取出的三个小球的所有可能结果;
(2)求![]() 的值是整数的概率.
的值是整数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被哦感染.
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
(3)![]() 轮(
轮(![]() 为正整数)感染后,被感染的电脑有________台.
为正整数)感染后,被感染的电脑有________台.
查看答案和解析>>
科目: 来源: 题型:
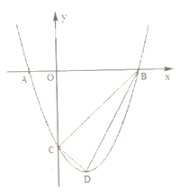
【题目】如图,抛物线![]() 与轴交于
与轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,设抛物线的顶点为点
,设抛物线的顶点为点![]() .
.
(1)求该抛物线的解析式与顶点![]() 的坐标.
的坐标.
(2)试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)坐标轴上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 购买江苏省体育彩票有“中奖”与“不中奖”两种情况,所以中奖的概率是![]()
B. 国家级射击运动员射靶一次,正中靶心是必然事件
C. 如果在若干次试验中一个事件发生的频率是![]() ,那么这个事件发生的概率一定也是
,那么这个事件发生的概率一定也是![]()
D. 如果车间生产的零件不合格的概率为![]() ,那么平均每检查1000个零件会查到1个次品
,那么平均每检查1000个零件会查到1个次品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com