
科目: 来源: 题型:
【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和3,点D在CE上,且∠A=120°,B,C,G三点在同一直线上,则BD与CF的位置关系是_____;△BDF的面积是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】对于题目“抛物线l1:![]() (﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
(﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
A.只有甲的结果正确
B.只有乙的结果正确
C.甲、乙的结果合起来才正确
D.甲、乙的结果合起来也不正确
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y=![]() 与y=
与y=![]() 的图象上分别有一点A,B,且AB∥x轴,AD⊥x轴于D,BC⊥x轴于C,若矩形ABCD的面积为8,则b﹣a=( )
的图象上分别有一点A,B,且AB∥x轴,AD⊥x轴于D,BC⊥x轴于C,若矩形ABCD的面积为8,则b﹣a=( )
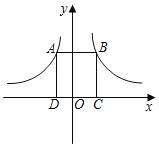
A.8B.﹣8C.4D.﹣4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在4×4的网格中,点A,B,C,D,H均在网格的格点上,下面结论:
①点H是△ABD的内心
②点H是△ABD的外心
③点H是△BCD的外心
④点H是△ADC的外心
其中正确的有( )
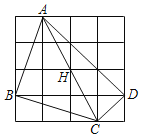
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=![]() x2+
x2+![]() x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)写出点A,B的坐标, 并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴上方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能求此时点P的坐标(直接写出结果);若不能,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C.
(1)求证:BE=CE;
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N,若AB=2.(如图2)
①求证:四边形EMBN的面积为定值;
②设BM=x,△EMN面积为S,求S最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表给出了代数式ax2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
ax2+bx+c | … | 3 |
| ﹣1 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=ax2+bx+c,则当x取何值时,y<0;
(3)当0<x<3,求x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
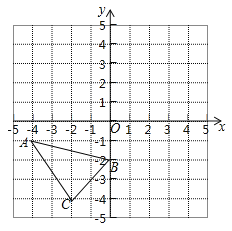
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com