
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目: 来源: 题型:
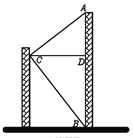
【题目】小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的水平距离CD的长度,小明从自己家的窗户C处测得∠DCA=37°,∠DCB=48°(DC平行于地面).求小明家所在居民楼与大厦的距离CD的长度.
(参考数据:sin37°![]() ,tan37°
,tan37°![]() ,sin48°
,sin48°![]() ,tan48°
,tan48°![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.
(1)张华用“微信”支付的概率是______.
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?
查看答案和解析>>
科目: 来源: 题型:
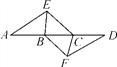
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:△AEC≌△DFB;
(2)若∠EBD=60°,BE=BC,求证:四边形BFCE是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,AD=2BD,ED与AB的延长线相交于点F,连接AD.
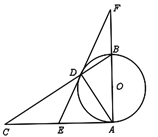
(1)求证:DE为⊙O的切线.
(2)求证:△FDB∽△FAD;
(3)若BF=2,,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( )
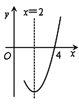
A.当x<2时,y随x增大而增大B.a-b+c<0
C.拋物线过点(-4,0)D.4a+b=0
查看答案和解析>>
科目: 来源: 题型:
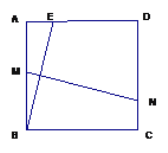
【题目】如图,在正方形ABCD中,AB=![]() ,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
(1)证明:MN = BE.
(2)设AE=![]() ,四边形ADNM的面积为S,写出S关于
,四边形ADNM的面积为S,写出S关于![]() 的函数关系式.
的函数关系式.
(3)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com