
科目: 来源: 题型:
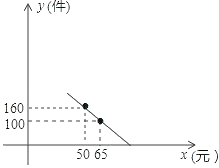
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件 40 元,经过记录分析发现,当销售单价在 40 元至 90 元之间(含40 元和 90 元)时,每月的销售量 y(件)与销售单价 x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求 y 与 x 的函数关系式.
(2)设商场老板每月获得的利润为P(元),求 P 与 x 之间的函数关系式;并求出利润的最大时销售单价为多少元?
(3)如果想要每月获得 2400 元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目: 来源: 题型:
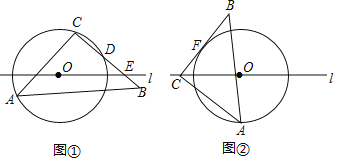
【题目】已知,△ABC中,∠ACB=90°,AC=BC=8,点A在半径为5的⊙O上,点O在直线l上.
(1)如图①,若⊙O经过点C,交BC于点D,求CD的长.
(2)在(1)的条件下,若BC边交l于点E,OE=2![]() ,求BE的长.
,求BE的长.
(3)如图②,若直线l还经过点C,BC是⊙O 的切线,F为切点,则CF的长为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于x的一元二次方程![]()
(1)求证:方程总有两个不相等的实数根。
(2)m为何整数时,此方程的两个根都是正整数?
(3)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求m的值。
查看答案和解析>>
科目: 来源: 题型:
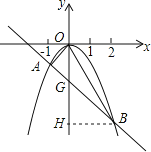
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),
(1)求二次函数和一次函数解析式.
(2)求△OAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
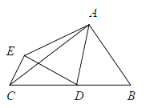
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目: 来源: 题型:
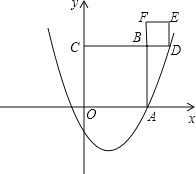
【题目】如图,抛物线![]() 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则E的坐标是____.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则E的坐标是____.
查看答案和解析>>
科目: 来源: 题型:
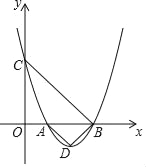
【题目】抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )
A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
查看答案和解析>>
科目: 来源: 题型:
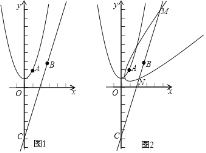
【题目】如图1,已知抛物线的顶点坐标为(0,1)且经过点A(1,2),直线y=3x﹣4![]() 经过点B(
经过点B(![]() ,n),与y轴交点为C.
,n),与y轴交点为C.
(1)求抛物线的解析式及n的值;
(2)将直线BC绕原点O逆时针旋转45°,求旋转后的直线的解析式;
(3)如图2将抛物线绕原点O顺时针旋转45°得到新曲线,新曲线与直线BC交于点M、N,点M在点N的上方,求点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
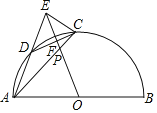
【题目】如图,在以AB为直径的半⊙O上有点C,点D在![]() 上,过圆心作OF⊥CD的于点F,OF、AD的延长线交于点E,连结CE,若∠DEC=90°.
上,过圆心作OF⊥CD的于点F,OF、AD的延长线交于点E,连结CE,若∠DEC=90°.
(1)试说明∠BAC=45°;
(2)若DF=1,△ACE的面积为△DCE面积的3倍,连接AC交OE于点P,求tan∠ACD的值和OP的长;
(3)在(2)的条件下,延长EC与AB的延长线相交于点G,直接写出BG的长 .
查看答案和解析>>
科目: 来源: 题型:
【题目】(知识回顾)
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
(理解应用)
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,试求m的值;
(2)若一次函数y=2kx+1﹣4k的图象经过某个定点,则该定点坐标为 ;
(能力提升)
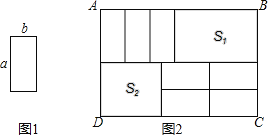
(3)7张如图1的小长方形,长为a,宽为b.按照图2方式不重叠地放在大矩形ABCD内,大矩形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变.求a与b的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com