
科目: 来源: 题型:
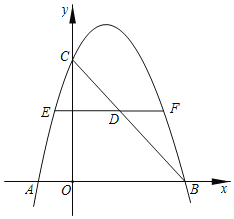
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
(1)求抛物线的对称轴和函数表达式.
(2)连结BC线段,BC上有一点D,过点D作x轴的平行线交抛物线于点E,F,若EF=6,求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD是⊙O的直径,以A为圆心,弦AB为半径画弧交⊙O于点C,连结BC交AD于点E,若DE=3,BC=8,则⊙O的半径长为( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线![]() 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
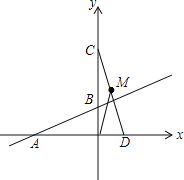
(1)点C的坐标是 ,线段AD的长等于 ;
(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点G,M,求抛物线的解析式;
(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)将![]() 绕着点
绕着点![]() 顺时针旋转90°,得到
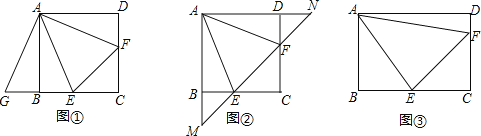
顺时针旋转90°,得到![]() (如图①),求证:
(如图①),求证:![]() ;
;
(2)若直线![]() 与
与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() (如图②),求证:
(如图②),求证:![]() ;
;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系 .(不要求书写证明过程)
之间的数量关系 .(不要求书写证明过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】武汉市雾霾天气严重,环境治理已刻不容缓,武汉市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台,若供应商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元/台)之间的函数关系式.
(元/台)之间的函数关系式.
(2)当售价![]() (元/台)定为多少时,商场每月销售这种空气净化器所获得的利润
(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(3)当售价![]() (元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润
(元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润![]() (元)不低于70000元?
(元)不低于70000元?
查看答案和解析>>
科目: 来源: 题型:
【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com