
科目: 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
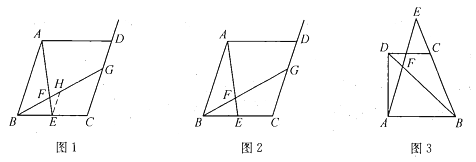
原题:如图1,在平行四边形![]() 中,点
中,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(1)尝试探究
在图1中,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 的值是______;
的值是______;
(2)类比延伸
如图2,在原题的条件下,当![]() 时,参照问题(1)的研究结论,请你猜想
时,参照问题(1)的研究结论,请你猜想![]() 的值(用含
的值(用含![]() 的代数式表示),并证明你的猜想;
的代数式表示),并证明你的猜想;
(3)拓展迁移
如图3,梯形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 和
和![]() 相交于点
相交于点![]() ,当
,当![]() ,
,![]() 时,请你求出
时,请你求出![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
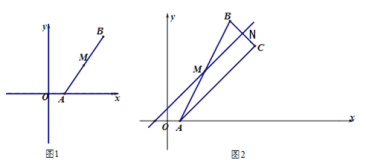
【题目】定义:在平面直角坐标系中,把点先向右平移1个单位,再向上平移2个单位的平移称为一次斜平移.已知点A(1,0),点A经过n次斜平移得到点B,点M是线段AB的中点.
(1)当n=3时,点B的坐标是 ,点M的坐标是 ;
(2)如图1,当点M落在![]() 的图像上,求n的值;
的图像上,求n的值;
(3)如图2,当点M落在直线![]() 上,点C是点B关于直线
上,点C是点B关于直线![]() 的对称点,BC与直线
的对称点,BC与直线![]() 相交于点N.
相交于点N.
①求证:△ABC是直角三角形
②当点C的坐标为(5,3)时,求MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC、AB相交于点D、E,连接AD,已知∠CAD=∠B.
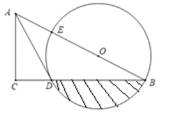
(1)求证:AD是⊙O的切线;
(2)若∠B=30°,AC=![]() ,求劣弧BD与弦BD所围阴影图形的面积;
,求劣弧BD与弦BD所围阴影图形的面积;
(3)若AC=4,BD=6,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价a元,则平均每天销售数量为 件.(用含a的代数式表示)
(2)当每件商品降价多少元时,该商店每天销售利润为1200元.
查看答案和解析>>
科目: 来源: 题型:
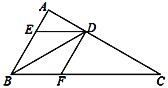
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
查看答案和解析>>
科目: 来源: 题型:
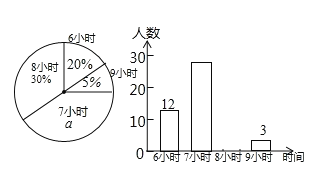
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确到1h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数a的值为 ,所抽查的学生人数为 .
(2)求出平均睡眠时间为8小时的人数,并补全频数直方图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目: 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com