
科目: 来源: 题型:
【题目】如图,直线y=2x﹣8分别交x轴、y轴于点A、点B,抛物线y=ax2+bx(a≠0)经过点A,且顶点Q在直线AB上.
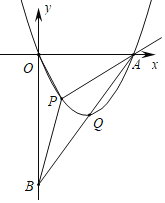
(1)求a,b的值.
(2)点P是第四象限内抛物线上的点,连结OP、AP、BP,设点P的横坐标为t,△OAP的面积为s1,△OBP的面积为s2,记s=s1+s2,试求s的最值.
查看答案和解析>>
科目: 来源: 题型:
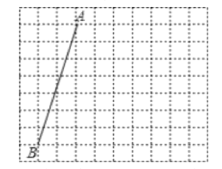
【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD点D在小正方形的项点上,且△ABD是锐角三角形。连接CD,请直接写出线段CD的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此,某校随机抽取了九年级(一)班的学生对安全知识的了解情况进行了一次调查统计图1和图2是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
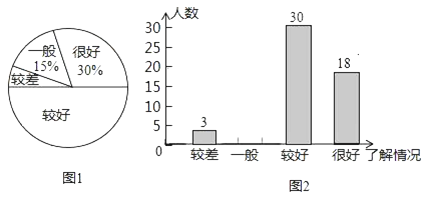
(1)此次调查共抽查了________名学生;
(2)补全统计图;
(3)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是________;
(4)若全校有1800名学生,估计对安全知识的了解情况为“很好”的学生共有________名.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)计算:(3﹣π)0﹣![]() +|3﹣
+|3﹣![]() |+(tan30°)﹣1
|+(tan30°)﹣1
(2)定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
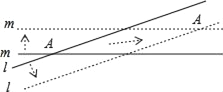
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
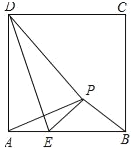
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图).
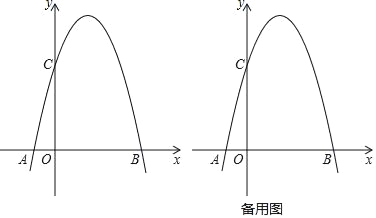
(1)求平移后的抛物线的表达式;
(2)如果点D在线段CB上,且CD=![]() ,求∠CAD的正弦值;
,求∠CAD的正弦值;
(3)点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 和
和![]() 是有公共顶点的直角三角形,
是有公共顶点的直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
(1)如图1,若![]() 和
和![]() 是等腰三角形,求证:
是等腰三角形,求证:![]() ;
;
(2)如图2,若![]() ,问:(1)中的结论是否成立?请说明理由.
,问:(1)中的结论是否成立?请说明理由.
(3)在(1)的条件下,若![]() ,
,![]() ,若把
,若把![]() 绕点A旋转,当
绕点A旋转,当![]() 时,求PB的长.
时,求PB的长.
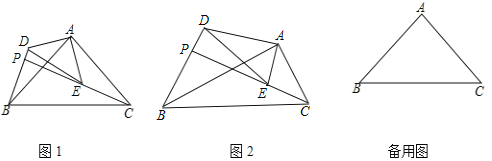
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售A、B两种品牌的教学设备,其进价分别为![]() 万元
万元![]() 套,
套,![]() 万元
万元![]() 套;售价分别为
套;售价分别为![]() 万元
万元![]() 套、
套、![]() 万元
万元![]() 套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.
套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.
(1)设该商场计划购进A、B两种品牌的教学设备各x套、y套,求x,y的值.
(2)调研后,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的![]() 倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?
倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com